Actualizado por ultima vez el 30 de noviembre de 2021, por Luis Benites.
¿Qué es el Lema de Neyman-Pearson?
El lema de Neyman-Pearson es una forma de averiguar si la prueba de hipótesis que estás utilizando es la que tiene mayor poder estadístico . La potencia de una prueba de hipótesis es la probabilidad de que la prueba rechace correctamente la hipótesis nula cuando la hipótesis alternativa es verdadera. El objetivo sería maximizar este poder, de modo que la hipótesis nula se rechace tanto como sea posible cuando la alternativa es verdadera. El lema básicamente nos dice que las buenas pruebas de hipótesis son pruebas de razón de verosimilitud .
El lema lleva el nombre de Jerzy Neyman y Egon Sharpe Pearson , quienes lo describieron en 1933. Muchos lo consideran el fundamento teórico de la teoría de la prueba de hipótesis, a partir del cual se construyen todas las pruebas de hipótesis.
Nota : Lemma parece que debería ser una letra griega, pero no lo es. En matemáticas, un lema se define como una proposición intermedia que se usa como un «peldaño» para algún otro teorema. Para diferenciar el lema de las teorías que tienen un nombre y una letra griega (como Delta de Glass o kappa de Fleiss ), a veces se escribe como Lema (Neyman-Pearson).
La Prueba de Hipótesis “Simple”
El lema de Neyman-Pearson se basa en una simple prueba de hipótesis. Una prueba de hipótesis «simple» es aquella en la que los parámetros desconocidos se especifican como valores únicos. Por ejemplo:
- H 0 : μ = 0 es simple porque la media poblacional se especifica como 0 para la hipótesis nula .
- H0 : µ = 0 ; H A : μ = 1 también es simple porque la media poblacional para la hipótesis nula y la hipótesis alternativa son valores únicos especificados. Básicamente, está asumiendo que los parámetros para esta prueba solo pueden ser 0 o 1 (lo cual es teóricamente posible si la prueba fuera binomial ).
En cambio, la hipótesis σ 2 > 7 no es simple; es una prueba de hipótesis compuesta que no establece un valor específico para σ 2 .
Las pruebas de hipótesis simples, incluso las optimizadas, tienen un valor práctico limitado . Sin embargo, son herramientas hipotéticas importantes; La prueba de hipótesis simple es sobre la que se construyen todas las demás.
La «mejor» región de rechazo
Como todas las pruebas de hipótesis, la prueba de hipótesis simple requiere una región de rechazo : el espacio de muestra más pequeño que define cuándo se debe rechazar la hipótesis nula. Esta región de rechazo (definida por el nivel alfa) podría tomar muchos valores. El lema de Neyman-Pearson básicamente nos dice cuándo hemos elegido la mejor región de rechazo posible.
La región de rechazo “Mejor” es aquella que minimiza la probabilidad de cometer un error Tipo I o Tipo II :
- Un error tipo I (α) es cuando rechazas la hipótesis nula cuando en realidad es cierta.
- Un error de tipo II (β) es cuando no se rechaza la hipótesis nula cuando es falsa.
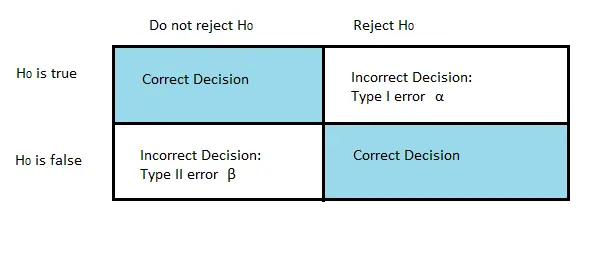 La probabilidad de que X esté en la región de rechazo R es la potencia estadística de la prueba. El escenario ideal sería que ambas probabilidades fueran cero o al menos extremadamente pequeñas . En el mundo real esto no es posible, porque una reducción de alfa a menudo conduce a un aumento de beta y viceversa. Pero podemos acercarnos, y para eso nos ayuda el lema.
La probabilidad de que X esté en la región de rechazo R es la potencia estadística de la prueba. El escenario ideal sería que ambas probabilidades fueran cero o al menos extremadamente pequeñas . En el mundo real esto no es posible, porque una reducción de alfa a menudo conduce a un aumento de beta y viceversa. Pero podemos acercarnos, y para eso nos ayuda el lema.
Definición del lema de Neyman-Pearson
Para entender el lema, es necesario definir algunos principios básicos sobre los niveles alfa/beta y la potencia:
Niveles Alfa y Beta
Un error Tipo I bajo la hipótesis nula se define como:
P θ (X ∈ R ∣ H 0 es verdadero),
Donde :
- R = la región de rechazo y
- ∈ es la pertenencia del conjunto.
Un error Tipo II bajo la hipótesis nula se define como:
P θ (X ∈ R c ∣ H 0 es falso),
Donde :
- R c = el complemento de R.
Por lo general, se establece un nivel alfa (por ejemplo, 0,05) para restringir la probabilidad de cometer un error de tipo I (α) a un cierto porcentaje (en este caso, 5%). A continuación, se elige una prueba que minimice los errores de tipo II (β).
Energía
Las pruebas con un cierto nivel alfa α se pueden escribir como:
Pruebas de tamaño α: sup β (θ) = α (θ ∈ Θ 0 )
donde :
- Θ 0 = conjunto de todos los valores posibles para θ bajo la hipótesis nula
Una prueba de nivel α es aquella que tiene la función de potencia más grande . Matemáticamente, se escribe como:
Prueba de nivel α: sup β (θ) ≤α(Θ ∈ Θ 0 )
Definiciones usando UMP y razón de verosimilitud
Casella y Berger (2002) utilizan las definiciones anteriores para definir una prueba de hipótesis simple que es uniformemente más poderosa (UMP) , que es la esencia del lema de Neyman-Pearson:
“Sea C una clase de pruebas para probar H 0 : θ ∈ Θ 0 versus H 1 : θ ∈ Θ c 1 . Una prueba en clase C, con función de potencia β(θ), es una prueba de clase C uniformemente más poderosa (UMP) si β(θ) ≥ β′(θ) para cada θ ∈ Θ 0 c y cada β′(θ) esa es una función de potencia de una prueba en la clase C.
En lenguaje sencillo, esto básicamente está diciendo:
El mismo enunciado también se puede presentar en términos de las pruebas de razón de verosimilitud . Digamos que tienes dos hipótesis simples H 0 : θ = θ 0 y H 1 :θ= θ 1 . Para encontrar la prueba más poderosa en un cierto nivel alfa (con umbral η), buscaría la prueba de razón de verosimilitud que rechaza la hipótesis nula a favor de la hipótesis alternativa cuando donde .
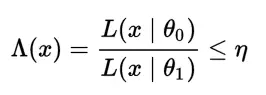
![]()
variantes
Existen docenas de formas diferentes del lema de Neyman-Pearson (NPL), cada una con notaciones y demostraciones diferentes. Incluyen variantes por:
- Roussas (1997): NPL fundamental para variables aleatorias continuas
- Casella y Berger (2002): NPL para variables aleatorias continuas y discretas
- Bain y Engelhardt (1990): NPL simplificada
- Lehmann (1991): una variante multidimensional de la NPL.
Referencias :
Bain, Lee J. y Max Engelhardt. Introducción a la Probabilidad y Estadística Matemática . 2ª ed. Boston: PWS-KENT Pub., 1992. Imprimir
Casella, George y Roger L. Berger. Inferencia Estadística . 2ª ed. Australia: Duxbury, 2002. Imprimir.
Hallin, M. Neyman-Pearson Lemma. Wiley StatsRef: Referencia de estadísticas en línea. 2014.
Lehmann, EL Contraste de hipótesis estadísticas. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced & Software, 1991. Impreso.
Roussas, George G. Un curso de estadística matemática. 2ª ed. San Diego, CA: Académico, 1997. Imprimir.

