Actualizado por ultima vez el 17 de diciembre de 2021, por Luis Benites.
El criterio Cp de Mallows es una forma de evaluar el ajuste de un modelo de regresión múltiple . Luego, la técnica compara el modelo completo con un modelo más pequeño con parámetros «p» y determina cuánto error queda sin explicar en el modelo parcial. O, más concretamente, estima el cuadrado medio total normalizado de estimación para el modelo parcial con la fórmula (Hocking, 1976): Donde:
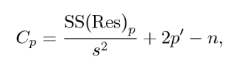
- SS(Res) p = suma residual de cuadrados de un modelo con un conjunto de p – 1 variables explicativas , más un intercepto (una constante),
- s 2 = estimación de σ 2
Un método común es realizar todas las regresiones posibles y luego usar el Cp de Mallows para comparar los resultados.
Cómo interpretar el Cp de Mallows
Se han hecho varias sugerencias sobre cómo se debe interpretar exactamente la estadística, pero el consenso general es que los valores de Cp más pequeños son mejores , ya que indican cantidades más pequeñas de error no explicado. Dicho esto, la estadística debe usarse en contexto, según su campo y conocimiento de los datos. Como cualquier método de ajuste de modelos, el «mejor» modelo no es necesariamente un modelo «razonable».
Una gráfica de Cp versus p (una constante) también puede ayudarlo a comparar modelos; Es posible que desee considerar solo modelos que tengan un Cp pequeño y un Cp cercano a p. Alternativamente, puede elegir el modelo más pequeño para el cual C p ≤ p es verdadero.
Las formas alternativas de evaluar el ajuste incluyen R 2 y r-cuadrado ajustado . Estos se utilizan a menudo junto con el Cp de Mallows para evaluar el ajuste del modelo. Otra alternativa, el Criterio de Información de Akaike (AIC) es equivalente al Cp de Mallows para la regresión lineal gaussiana (Boisbunon, 2013).
Referencias
Boisbunon, A. et al. (2013). “AIC, Cp y estimadores de pérdida para distribuciones elípticamente simétricas”. arXiv:1308.2766 [matemáticas.ST].
Gilmour, S. La interpretación del $C_p$-Estadístico de Mallows. Revista de la Real Sociedad Estadística. Serie D (El Estadístico). vol. 45, No. 1 (1996), pp. 49-56
Hocking, R. El Análisis y Selección de Variables en Regresión Lineal. Biometría, 32:1-49.
Hobbs, G. Construcción de modelos: Criterios de selección . Recuperado el 5 de marzo de 2020 de: https://www.stat.purdue.edu/~ghobbs/STAT_512/Lecture_Notes/Regression/Topic_15.pdf

