Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 21 de mayo de 2022, por Luis Benites.
Es posible que desee leer este artículo primero: ¿Qué es la media recortada?
¿Qué es la media intercuartil?
La media intercuartil (IQM) es la media del 50 por ciento medio de los datos en un conjunto de datos. A diferencia de la media aritmética «regular» , es resistente a los valores atípicos .
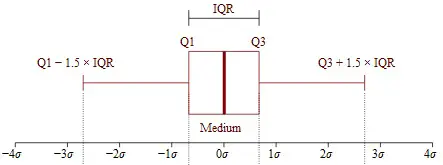
El IQM es la media del rango intercuartil (IQR).
Cómo encontrar la media intercuartil
El cálculo es diferente dependiendo de si tus datos son divisibles por 4 o no.
Los datos son divisibles por cuatro
Pregunta de ejemplo: encuentre el IQM para el siguiente conjunto de datos:
5 6 17 30 44 55 56 8 9 11 13 15 1 3 16 65
Paso 1: ordene los datos de menor a mayor:
1 3 5 6 8 9 11 13 15 16 17 30 44 55 56 65
Paso 2: Deseche el 25% inferior y el 25% superior de los números. En otras palabras, divida el conjunto de datos en cuartos y elimine los cuartos superior e inferior:
1 3 5 6 | 8 9 11 13 | 15 16 17 30 | 44 55 56 65
Paso 3: Encuentra la media de los números restantes:
(8 + 9 + 11 + 13 + 15 + 16 + 17 + 30) / 8 = 14.875
¡Eso es todo!
Los datos NO son divisibles por cuatro
Pregunta de ejemplo: encuentre el IQM para el siguiente conjunto de datos:
6 17 30 44 55 56 8 9 11 13 15 1 3 16 65
Paso 1: ordene los datos de menor a mayor:
1 3 6 8 9 11 13 15 16 17 30 44 55 56 65
Paso 2: Divida el número de artículos en el conjunto por cuatro. El conjunto tiene 15 elementos, por lo que 15/4 = 3,75.
Paso 3: Retire el número entero (Paso 2) de la parte inferior y superior del conjunto. Para este ejemplo, el número entero es 3 (de 3,75):
1 3 6 8 9 11 13 15 16 17 30 44 55 56 65
que sale:
8 9 11 13 15 16 17 30 44
Paso 4: Calcule cuántos elementos hay en el rango intercuartílico . El IQR son los dos cuartos del medio, por lo que habría 3,75 * 2 = 7,5 números.
Paso 5: Coloque paréntesis alrededor del conjunto de números del medio usando el número entero del Paso 4. En este ejemplo, el número entero es 7:
8 (9 11 13 15 16 17 30) 44
Paso 6: Tome la parte fraccionaria del Paso 4 (.5 en este caso) y divídala por dos (porque hay dos números fuera de los paréntesis):
.5/2 = .25
Esto significa que los números 8 y 44 contribuirán cada uno con un 25% al IQM.
Paso 7: Multiplique los dos números «externos» (8 y 44 en este caso) por la fracción en el Paso 6:
8 * .25 = 2
44 * .25 = 11
Paso 8: Reemplace los dos números externos por los números fraccionarios (Paso 7) y encuentre la media. Al dividir por «n», use la cantidad de elementos en el IQR del Paso 4 (7.5 en este caso), no el número real (9 en este ejemplo):
8 2 (9 11 13 15 16 17 30) 44 11 =
(2 + 9 + 11 + 13 + 15 + 16 + 17 + 30 + 11)/7,5 = 16,53.
¡Eso es todo!
Referencias
Salkind, N. (2008). Enciclopedia de Diseño de Investigación . SABIO.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
