Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 14 de octubre de 2021, por Luis Benites.
Es posible que desee leer este artículo primero: Tasas de error de Familywise.
¿Qué es el Método Holm-Bonferroni?
El Método Holm-Bonferroni (también llamado Procedimiento Secuencial de Bonferroni de Holm) es una forma de tratar con las tasas de error familiar (FWER) para pruebas de hipótesis múltiples . Es una modificación de la corrección de Bonferroni . La corrección de Bonferroni reduce la posibilidad de obtener un resultado estadísticamente significativo (es decir, un error de tipo I) al realizar varias pruebas. Aunque el Bonferroni es simple de calcular, adolece de una falta de poder estadístico . El método Holm-Bonferroni también es bastante simple de calcular, pero es más poderoso que el Bonferroni de un solo paso.
Fórmula
La fórmula para calcular el Holm-Bonferroni es: Donde :
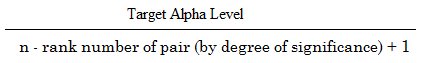
- Nivel alfa objetivo = nivel alfa general (generalmente .05),
- n = número de pruebas.
El siguiente ejemplo muestra cómo funciona la fórmula.
Ejemplo
Pregunta : Use el método Holm-Bonferroni para probar las siguientes cuatro hipótesis y sus valores p asociados en un nivel alfa de .05:
- H1 = 0,01 .
- H2 = 0,04
- H 3 = 0,03
- H4 = 0,005
Nota : ya conocemos los valores de p asociados con cada hipótesis. Si no conoce los valores p, realice una prueba para cada hipótesis antes de intentar ajustar FWER utilizando el método Holm-Bonferroni.
Paso 1: ordene los valores p de menor a mayor:
- H4 = 0,005
- H1 = 0,01
- H 3 = 0,03
- H2 = 0,04
Paso 2: Trabajar la fórmula de Holm-Bonferroni para el primer rango:
HB = Objetivo α / (n – rango + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.
Paso 3: Compare el valor p clasificado en primer lugar (más pequeño) del Paso 1 con el nivel alfa calculado en el Paso 2:
Valor p más pequeño, en el Paso 1 (H 4 = 0,005) < Nivel alfa en el Paso 2 (0,0125) .
Si el valor p es menor, rechace la hipótesis nula para esta prueba individual.
El valor p de .005 es menor que .0125, por lo que se rechaza la hipótesis nula para H 4 .
Paso 4: Repita la fórmula HB para el segundo rango .
HB = Objetivo α / (n – rango + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167
Paso 5: Compare el resultado de la fórmula HB en el Paso 4 con el segundo valor p clasificado:
Segundo valor p clasificado, en el Paso 1 (H 1 = 0.01) < Nivel alfa en el Paso 2 (.0167).
El valor p de .01 es menor que .0167, por lo que también se rechaza la hipótesis nula para H 1 .
Paso 6: Repita la fórmula HB para el tercer rango .
HB = Objetivo α / (n – rango + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025
Paso 7: Compare el resultado de la fórmula HB en el Paso 6 con el valor p clasificado en
tercer lugar: Valor p clasificado en tercer lugar, en el Paso 1 (H 3 = 0.03) > Nivel alfa en el Paso 6 (.025).
El valor p de .03 es mayor que .025, por lo que no se rechaza la hipótesis nula para H 3 .
La prueba se detiene cuando llega a la primera hipótesis no rechazada. Todas las hipótesis posteriores no son significativas (es decir, no se rechazan).
Referencia :
Holm, S. 1979. Un procedimiento de prueba múltiple rechazante secuencial simple. Revista Escandinava de Estadística 6:65-70
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
