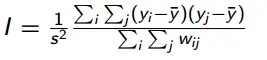I de Moran: definición, ejemplos

Actualizado el 11 de febrero de 2022, por Luis Benites.

I de Moran

¿Qué es el I de Moran?

El I de Moran es un coeficiente de correlación que mide la autocorrelación espacial general de su conjunto de datos. En otras palabras, mide cómo un objeto es similar a otros que lo rodean. Si los objetos se atraen (o repelen) entre sí, significa que las observaciones no son independientes . Esto viola una suposición básica de las estadísticas: la independencia de los datos. En otras palabras, la presencia de autocorrelación invalida la mayoría de las pruebas estadísticas, por lo que es importante probarla. Moran’s I es una forma de probar la autocorrelación.

La autocorrelación espacial es multidireccional y multidimensional, lo que la hace útil para encontrar patrones en conjuntos de datos complicados. Es similar a los coeficientes de correlación , tiene un valor de -1 a 1. Sin embargo, mientras que otros coeficientes miden una correlación perfecta o ninguna correlación, el de Moran es ligeramente diferente (debido a los cálculos espaciales más complejos):

• -1 es un agrupamiento perfecto de valores diferentes (también puede pensar en esto como una dispersión perfecta).
• 0 no es autocorrelación (aleatoriedad perfecta).
• +1 indica un agrupamiento perfecto de valores similares (es lo opuesto a la dispersión).

Dispersión Perfecta

En la imagen de arriba, los cuadrados en blanco y negro tienen un patrón definido y están perfectamente dispersos. El valor de Moran sería igual a -1.

Perfecta aleatoriedad

Si los cuadrados estuvieran verdaderamente dispersos al azar, el valor de Moran sería 0.

Agrupamiento perfecto

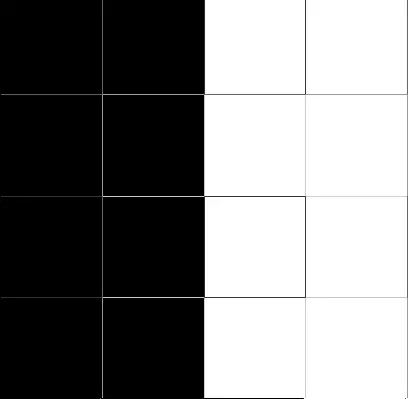
Esta imagen muestra que los cuadrados blancos y los cuadrados negros ocupan la mitad del área, a ambos lados del centro. Esta es una agrupación perfecta de valores similares, lo que da un valor de Moran de +1.

Evaluación del índice

El I de Moran se diferencia de la mayoría de los otros coeficientes de correlación en que no se puede tomar el índice al pie de la letra. Es una estadística inferencial y debe determinar la importancia estadística antes de poder leer el resultado. Esto se hace con una prueba de hipótesis simple , calculando un puntaje z y su valor p asociado .

• La hipótesis nula de la prueba es que los datos se distribuyen aleatoriamente.
• La hipótesis alternativa es que los datos están más agrupados espacialmente de lo que cabría esperar solo por casualidad. Dos escenarios posibles son:
  1. Un valor z positivo: los datos están agrupados espacialmente de alguna manera.
  2. Un valor z negativo: los datos se agrupan de forma competitiva. Por ejemplo, los valores altos pueden repeler los valores altos o los valores negativos pueden repeler los valores negativos.

Cálculos

Los cálculos del I de Moran se basan en una matriz ponderada, con unidades i y j. Las similitudes entre unidades se calculan como el producto de las diferencias entre y _i e y _j con la media global.

• Similitud = (y _i – ̄y)(y _j – ̄y), donde ̄y = Σ ⁿ _i=1 y _i /n
• El estadístico de Moran se calcula utilizando la forma básica, que se divide por la varianza de la muestra: s ² = (Σ(y _i – ̄y) ² )/n).