Actualizado por ultima vez el 2 de diciembre de 2021, por Luis Benites.
La mediana muestral es el «medio» de un conjunto de datos muestrales ordenados. Por ejemplo, supongamos que tiene una muestra de 5 puntos de datos: 1, 2, 4, 7 y 9. La mediana de la muestra es el número central:
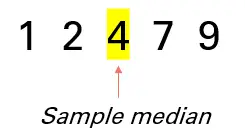
Cómo encontrar la mediana de la muestra
En general, coloca los números en orden de menor a mayor, luego encuentra el número del medio. Sin embargo, la fórmula exacta que utilice depende de si tiene un conjunto de números pares o impares [1]:
- Conjunto par de puntos de datos : Promedio de los valores en las posiciones n/2 y n/2 + 1,
- Conjunto impar de puntos de datos : el valor en la posición (n + 1)/2.
Donde “n” es el número de puntos de datos.
Mire el video para ver dos ejemplos con un conjunto impar de números y un conjunto par de números:
Media Mediana Moda 
Mira este video en YouTube .
Ventajas y desventajas de la mediana muestral
Una ventaja de la mediana de la muestra sobre la media de la muestra es que, dado que solo usa los dos números del medio, la estadística no se ve afectada por los valores atípicos .
La mediana de la muestra puede ser una buena medida de tendencia central si sus datos provienen de una distribución sesgada . Si tiene una distribución simétrica (como una distribución normal ), la media muestral puede ser una mejor opción.
Prueba para la mediana de la muestra
Cuantos más puntos de datos («n») tenga en una muestra, más cerca estará la mediana de su muestra de la verdadera mediana de la población. Pero es posible que desee saber con cierta certeza que su estadística calculada es igual a un valor de población real. Para hacer esto, ejecute una prueba de mediana de una muestra .
Referencias
[1] Sheldon M. Ross, en Introducción a la probabilidad y la estadística para ingenieros y científicos (quinta edición), 2014
