Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 24 de septiembre de 2021, por Luis Benites.
Contenidos:
No
linealidad Aditividad
no linealidad
Una no linealidad es una relación entre puntos de datos que no se pueden condensar en un gráfico lineal ordenado .
No linealidad frente a linealidad
Para comprender la no linealidad, primero debemos definir qué significa que la relación entre dos variables sea lineal .
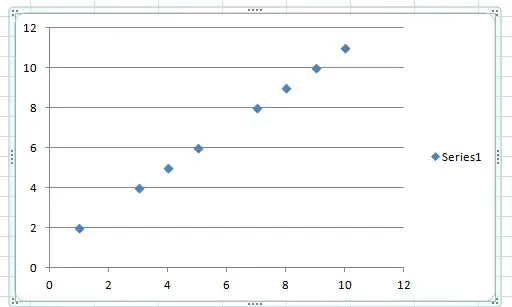
Variables en un diagrama de dispersión que muestra una relación lineal.
La linealidad es más fácil de entender visualmente. Si sus datos son lineales, puede graficarlos en un diagrama de líneas, como el de arriba. Con la concesión de un término de error , podrá trazar una línea ordenada a través de sus puntos.
Un pequeño cambio en su variable independiente (entrada) conducirá a un pequeño cambio en su variable dependiente (salida). Un gran cambio en su variable independiente conducirá a un gran cambio en su variable dependiente. A esto lo llamamos proporcionalidad .
Aditividad
La otra propiedad clave de las funciones lineales es la aditividad : : f(x + y) = f(x) + f(y). Básicamente, esto significa que puedes:
- Superponga las diferentes contribuciones a su variable independiente (entrada) con una suma simple.
- Divide tu salida para reflejar qué partes de la salida dependen de qué partes diferentes de la entrada.
- Divide tu problema para analizarlo, utilizando los principios básicos de suma y resta.
No linealidades: cuando cambian las reglas
Si la aditividad y la proporcionalidad caracterizan la linealidad, las no linealidades son desviaciones de al menos una de esas dos cosas. Deje que la relación entre su variable rompa la regla de proporcionalidad o los principios de aditividad y tendrá una no linealidad.
Pequeños cambios de entrada pueden conducir a grandes cambios de salida y grandes cambios de entrada a pequeños cambios de salida. O es posible que no pueda separar partes de su entrada (variable independiente) y salida para el análisis.
Los sistemas no lineales pueden ser caóticos o simplemente pueden necesitar un modelo más complicado que un diagrama de líneas básico.
Ejemplos de no linealidades en ciencia y estadística
La turbulencia de fluidos, la combustión y las reacciones bioquímicas que ocurren en los organismos vivos son solo algunos ejemplos de los muchos sistemas que investigamos hoy que exhiben no linealidades.
En estadística, la regresión no lineal es una forma de encontrar una aproximación no lineal para datos que no se ajustan al análisis lineal tradicional. (Vea abajo)
Modelos de regresión lineal y no lineal
Identificar modelos de regresión lineales y no lineales no es tan fácil como buscar líneas rectas, porque los modelos de regresión lineal pueden incluir curvas. Básicamente, un modelo de regresión lineal se define como una curva que se puede escribir como la suma de una constante y parámetros de primer orden multiplicados por variables.
Y = un 0 + segundo 1 X 1 + segundo 2 X 2 + segundo 3 X 3 …
Para ser un modelo de regresión lineal, los parámetros (b 1 , b 2 , b 3 deben ser de primer orden cada uno. Pero las variables (X 1 , X 2 , X 3 ) se pueden elevar al cuadrado, al cubo o a la n-ésima potencia, así que esto podría ser en realidad la ecuación de una curva. Incluso podría tomar el logaritmo o el inverso de la variable independiente, y esto no afectaría la linealidad del modelo de regresión si los parámetros son lineales (primer orden).
Si su modelo de regresión no se puede escribir Y = a 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 … , es un modelo no lineal.
Fuentes
Optimización lineal y no lineal
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
