Actualizado por ultima vez el 8 de diciembre de 2021, por Luis Benites.
El principio de máxima entropía es una regla que nos permite elegir el «mejor» de una serie de distribuciones de probabilidad diferentes que expresan el estado actual del conocimiento. Nos dice que la mejor elección es la de máxima entropía.
Este será el sistema con la mayor incertidumbre restante y, al elegirlo, se asegura de no agregar sesgos adicionales o suposiciones innecesarias en su análisis.
Sabemos que todos los sistemas tienden hacia configuraciones de entropía máxima a lo largo del tiempo, por lo que la probabilidad de que su sistema esté representado con precisión por la distribución de entropía máxima es mayor que la probabilidad de que esté representado por un sistema más ordenado.
Aplicación del principio de máxima entropía
La aplicación del principio de máxima entropía a un problema físico generalmente implica resolver algebraicamente una serie de ecuaciones para una serie de incógnitas.
Por ejemplo, considere el caso discreto en el que le gustaría averiguar la probabilidad de que una cantidad tome los valores {a, b, c, d…}. Todas las probabilidades sumarán uno; entonces tu primera ecuación es p(a) + p(b) + p(c) + p(d)… = 1.
Es posible que conozca alguna información sobre la situación; si lo hace, eso va en otra ecuación, llamada restricciones .
Ejemplo específico
Digamos que su investigación fue sobre la probabilidad de que la gente compre manzanas, plátanos o naranjas. Si compraran uno de tres en un supermercado en particular, sabrías:
1 = P manzana + P plátano + P naranjas .
Si también sabes que las manzanas cuestan un dólar cada una, las bananas dos dólares y las naranjas tres dólares, y si sabes que el precio promedio de la fruta comprada en el supermercado es de $1.75, sabrás
$1.75 = $1.00 P manzana + $2.00 P plátano + $3.00 P naranjas .
Eso es lo que llamamos nuestra ecuación de restricción. Esta podría ser toda la información que tienes. Pero con dos ecuaciones y tres incógnitas, simplemente no es suficiente información para llegar a una solución única. Ahí es donde entra en juego el principio de máxima entropía. El principio de máxima entropía reduce el espacio de todas las soluciones potencialmente posibles, y hay muchas, a la mejor solución; el de mayor entropía.
Llame a la entropía del sistema S. Sabemos que la entropía de Shannon se define como: El logaritmo , log b (1/p(A) i ) representa la información en el estado i, por lo que cuando se multiplica por p(A) i para cada i, obtenemos una medida de incertidumbre. Así que nuestra tercera ecuación es esta:
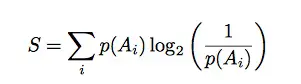
S = P manzana log 2 (1/ P manzana ) + P banana log 2 (1/ P banana ) + P naranja log 2 (1/ P naranja ).
Ahora el resto es solo álgebra.
Pasos de álgebra
Multiplicar cada término en tu primera ecuación por -$1.00 significa que, cuando lo sumas a tu ecuación de restricción, P manzana cae y tienes una ecuación con solo P banana y P naranja .
$0.75 = $1.00P plátano + $2.00P naranja
entonces podemos escribir P plátano en términos de P naranja así:
P plátano = 0,75 – 2,00 P naranja .
Podríamos escribir P manzana en términos de P naranja si, en lugar de multiplicar la ecuación 1 por -$1,00 para empezar, multiplicamos por -$2,00. Entonces tendríamos
-$0.25 = -$1.00P manzana + 1.00P naranja
que nos da
P manzana = P naranja + 0,25.
Pasos finales
Ahora podemos volver a nuestra tercera ecuación, aquella en la que todas las probabilidades suman entropía, y podemos escribir todas las demás probabilidades en términos de P naranja usando las dos ecuaciones que acabamos de derivar.
S = (P naranja + 0,25) log 2 (1/ (P naranja 0,25)) + (0,75 – 2 P naranja )log 2 (1/ (0,75- 2P naranja )) + P naranja log 2 (1/ P naranja )
Ahora todo lo que queda es encontrar el valor de P naranja para que S se maximice. Puede usar cualquiera de varios métodos para hacer esto; encontrar los puntos críticos de la función es una buena. Encontramos que la entropía se maximiza cuando P naranja = (3.25 – √3.8125) /6, que es aproximadamente 0.216.
Usando las ecuaciones anteriores, podemos concluir que P manzana es 0.466 y P plátano es 0.318.
Extendiendo el principio de máxima entropía a sistemas más grandes
Agregar una consideración de entropía puede definir completamente la situación si tenemos tres variables y solo una restricción, como se indicó anteriormente. Pero qué pasa en situaciones más complicadas; por ejemplo, donde tiene más de tres variables? Es un supermercado mal abastecido que solo vende naranjas, plátanos y manzanas. ¿Qué pasaría si las uvas y el melón estuvieran entre otras opciones?
Resulta que el principio de máxima entropía también puede definir completamente esta situación. Además de usar las ecuaciones utilizadas anteriormente, también puede usar: Primero, necesitamos definir dos nuevas incógnitas, α y β, que se denominan multiplicadores de Legrange . Luego usamos la función de Lagrange Aquí, e es la base del logaritmo natural, 2.7183, por lo que log 2 e es solo 1.4427. Para encontrar probabilidades desconocidas en un caso como el anterior, resolvemos nuestra colección de ecuaciones para que L se maximice. Esto también maximiza a nuestro viejo amigo S, la entropía.
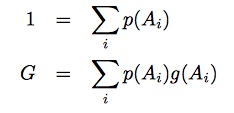
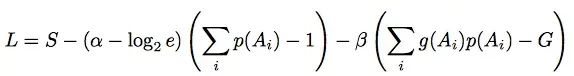
Referencias
Penfield, Paul. Información y entropía Apuntes de clase: Capítulo 9: Principio de máxima energía: forma simple y Capítulo 10: Principio de máxima entropía. Recuperado de: https://mtlsites.mit.edu/Courses/6.050/2003/notes/chapter9.pdf chapter10.pdf el 19 de febrero de 2018
Xie, Yao. ECE587 Teoría de la información Notas de clase: Clase 11, Entropía máxima. Recuperado el 1 de marzo de 2018 de:
https://www2.isye.gatech.edu/~yxie77/ece587/Lecture11.pdf el 19 de febrero de 2018
