Actualizado por ultima vez el 22 de febrero de 2022, por Luis Benites.
Un intervalo creíble es el intervalo en el que un parámetro (no observado) tiene una probabilidad determinada.
Es el equivalente bayesiano del intervalo de confianza que probablemente haya encontrado antes. Sin embargo, a diferencia de un intervalo de confianza, depende de la distribución previa (específica de la situación). En los intervalos de confianza también tratamos el parámetro como un valor fijo y los límites son variables aleatorias ; en intervalos creíbles, el parámetro estimado se trata como una variable aleatoria mientras que los límites se consideran fijos.
Ejemplos de intervalos creíbles
Supongamos que estamos realizando un experimento sobre la distribución de los pesos al nacer de los niños nacidos en un pueblo determinado. Si la probabilidad subjetiva de que el peso al nacer β esté entre 2,8 kg y 3,5 es del 90 %, podemos decir que 2,8 ≤ β ≤ 3,5 es un intervalo creíble del 90 %.
Si descubre que el intervalo creíble del 95 % para la puntuación final de sus estadísticas es de 70 a 90, significa que tiene un 95 % de posibilidades de obtener una puntuación entre esos dos números.
Definición técnica de un intervalo creíble
Recuerde que un nivel alfa , α, define la cantidad de incertidumbre; la probabilidad de que apoyemos la hipótesis alternativa cuando en realidad la hipótesis nula es verdadera. Podemos decir que nuestro intervalo de credibilidad 100 (1 – α) % C define el subconjunto en el espacio de parámetros , que llamaremos θ, tal que la integral
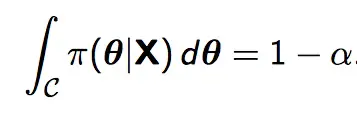
π aquí es la distribución de probabilidad posterior . Entonces, por ejemplo, si necesita un intervalo creíble del 95 por ciento, estaría trabajando para encontrar el intervalo sobre el cual la integral de la distribución de probabilidad posterior suma 0,95.
Hay un atajo que a veces podemos tomar. Si el espacio de parámetros θ es un espacio discreto, es decir, si estamos trabajando con un conjunto de puntos de datos discretos en lugar de una distribución continua, podemos sumar sobre nuestro intervalo en lugar de tomar una integral.
Referencias
Hitchcok, David. Inferencia bayesiana: Intervalos posteriores (Stat 535 Lecture Notes)
Obtenido de http://people.stat.sc.edu/Hitchcock/stat535slidesday3.pdf el 16 de febrero de 2018
Jaynes, ET (1976). “Intervalos de confianza frente a intervalos bayesianos”, en Fundamentos de la teoría de la probabilidad, inferencia estadística y teorías estadísticas de la ciencia, págs. 175 y siguientes. Recuperado de http://bayes.wustl.edu/etj/articles/confidence.pdf el 17 de febrero de 2018

