Contenido de este artículo
Actualizado el 4 de abril de 2022, por Luis Benites.
¿Qué es la probabilidad inversa?
La probabilidad inversa es la probabilidad de cosas que no se observan; o, más técnicamente, la distribución de probabilidad de una variable no observada. Generalmente se considera un término obsoleto.
Hoy en día, la base de la probabilidad inversa (determinar la variable no observada) suele denominarse estadística inferencial , y el principal problema de la probabilidad inversa (encontrar una distribución de probabilidad para una variable no observada) suele denominarse probabilidad bayesiana .
Probabilidad inversa, también conocida como probabilidad bayesiana: en qué consiste
La probabilidad bayesiana se usa a menudo cuando queremos calcular la probabilidad de ciertos resultados dada una hipótesis particular . Es una forma de convertir los problemas de inferencia lógica en problemas estadísticos simples, observando las probabilidades condicionales y comparando los resultados dados diferentes escenarios hipotéticos.
La fórmula de la regla de Bayes es:
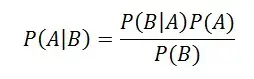
La regla se puede escribir con una notación ligeramente diferente para ilustrar la conexión entre una hipótesis y una condición:
Aquí P(H|D) es la probabilidad de que la hipótesis H sea verdadera dada una condición particular D, P(D|H) es la probabilidad de que la condición D sea verdadera dada la hipótesis siendo verdadera, y P(H) y P( D) son las probabilidades de observar la hipótesis y la condición D, independientemente una de la otra.
Mire el video para ver un ejemplo rápido de cómo resolver un problema del Teorema de Bayes, o lea un problema de ejemplo diferente a continuación:
Mira este video en YouTube .
Ejemplo de probabilidad inversa simple: aplicación de la regla de Bayes
Una prueba de detección de una anomalía genética en particular es muy eficaz; da un 99 % de resultados positivos verdaderos para quienes portan la anomalía y un 95 % de resultados negativos verdaderos para quienes no la tienen. Solo un porcentaje muy pequeño de la población general, el 0,001%, es portador de esta anomalía genética.
La probabilidad inversa y la regla de Bayes nos permiten calcular cuál es la probabilidad de que alguien al azar tenga la anomalía genética, dada una prueba positiva. La anormalidad genética es la hipótesis, y la prueba positiva es nuestra condición. En nuestra fórmula anterior, querremos conectar los valores:
P(D|H) = 0,99
P(H) = 0,00001
P(D), o la probabilidad de una prueba positiva, es solo la suma de dos términos. El primer término es la probabilidad de una prueba positiva dada la anomalía genética multiplicada por la probabilidad de que exista la anomalía. El segundo término será la probabilidad de una prueba positiva si no hay anomalía genética, multiplicada por la probabilidad de que no haya anomalía genética. Entonces:
P(D) = P(D|H) P(H) + P(D|~H) P(~H).
Eso equivale a 0,99*0,00001 + 0,01*0,99999 o 0,0100098.
Reemplazando estos en la fórmula anterior para la regla de Bayes, obtenemos:
P(H|D) = [0,99*0,00001] / 0,0100098
O, sin tener en cuenta los dígitos significativos , 0.00098903074. Vemos que aunque la prueba puede ser bastante confiable, la anomalía genética es tan rara que incluso una prueba positiva solo deja a una persona con solo un 0,09 por ciento de probabilidad de tener la anomalía.
¿Qué es una distribución inversa?
“Distribución inversa” es uno de esos términos que tiene varios significados, dependiendo de dónde lo estés leyendo. Es uno de esos términos informales que significa una cosa si está trabajando con muestreo en estadísticas , otra si está mirando funciones de distribución acumulativas y otra más si las variables en una distribución son recíprocas. Según el Oxford Dictionary of Statistical Terms, las diferentes definiciones incluyen:
- El recíproco de la distribución de probabilidad de una variable aleatoria . Por ejemplo, la distribución gamma inversa es el recíproco de la distribución gamma .
- Muestreo hasta un cierto número de aciertos. Ver : Muestreo inverso .
- Distribuciones donde las frecuencias son cantidades recíprocas (por ejemplo, la distribución factorial),
- Como una forma de encontrar variables en términos de la función de distribución F(x). Por ejemplo, la distribución normal inversa se refiere a la técnica de trabajar hacia atrás, dada F(x) para encontrar los valores de x.
Si bien todas las definiciones son usos válidos del término «Distribución inversa», el término » Función de distribución inversa » por lo general implica la definición #4, es decir, usarlo para encontrar probabilidades.
Siguiente : Problemas del Teorema de Bayes.
Referencias
Olshausen, B. (2004). Teoría de la probabilidad bayesiana . Recuperado el 5 de diciembre de 2017 de http://redwood.berkeley.edu/bruno/npb163/bayes.pdf.
Teorema de Bayes, Enciclopedia de Filosofía de Stanford
https://plato.stanford.edu/entries/bayes-theorem/
