Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 5 de septiembre de 2021, por Luis Benites.
¿Qué es la prueba de Bartlett?
En realidad, hay dos pruebas llamadas de Bartlett. La primera parte de este artículo es para la prueba de homogeneidad de varianzas de Bartlett . Si está buscando la prueba de esfericidad de Bartlett (probar que la matriz de correlación tiene una matriz de identidad ), salte a la sección inferior .
La prueba de homogeneidad de varianzas de Bartlett se usa para probar que las varianzas son iguales para todas las muestras. Comprueba que la suposición de varianzas iguales sea cierta antes de ejecutar ciertas pruebas estadísticas como el ANOVA de una vía . Se usa cuando está bastante seguro de que sus datos provienen de una distribución normal . Una prueba similar, llamada prueba de Levene , es una mejor opción para distribuciones no normales .
La hipótesis nula de la prueba es que las varianzas son iguales para todas las muestras. En términos estadísticos, eso es:
H 0 : σ 1 2 = σ 2 2 = … = σ k 2 .
La hipótesis alternativa (la que está probando) es que las varianzas no son iguales para un par o más:
H 0 : σ 1 2 ≠ σ 2 2 ≠… ≠ σ k 2 .
La estadística de la prueba es bastante fea: es por eso que lo más probable es que desee usar software para la prueba.
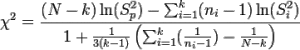
- Instrucciones para R.
- Excel no tiene una función integrada, pero puede descargar esta hoja de trabajo de prueba de Bartlett y completar los espacios en blanco (Hoja de trabajo descargada de John McDonald en la Universidad de Delaware ).
- En STATA, el de Bartlett se agrega a ANOVA. La sintaxis básica del comando es oneway dv iv donde iv es una variable categórica . Para obtener más información sobre cómo ejecutar la prueba en STATA, consulte este artículo de Notre Dame .
Si realmente desea ejecutar la prueba de Bartlett a mano, consulte este artículo , que explica cómo hacerlo con gran detalle.
Prueba de Bartlett para la esfericidad
La prueba de Bartlett para la esfericidad compara su matriz de correlación (una matriz de correlaciones de Pearson ) con la matriz de identidad. En otras palabras, comprueba si hay redundancia entre variables que se pueden resumir con algunos factores.
- En IBM SPSS 22, puede encontrar la prueba en el menú Descriptivos: Analizar-> Reducción de dimensión-> Factorizar-> Descriptivos-> KMO y prueba de esfericidad de Bartlett.
- Instrucciones en R.
Referencia :
Snedecor, George W. y Cochran, William G. (1989), Métodos estadísticos, octava edición, Iowa State University Press.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
