Contenido de este artículo
Actualizado el 24 de octubre de 2021, por Luis Benites.
¿Qué es la prueba de Dunnett?
La prueba de Dunnett (también llamada método de Dunnett o comparación múltiple de Dunnett) compara las medias de varios grupos experimentales con la media de un grupo de control para ver si hay una diferencia. Cuando una prueba ANOVA tiene hallazgos significativos , no informa qué pares de medias son diferentes. La prueba de Dunnett se puede utilizar después de ejecutar el ANOVA para identificar los pares con diferencias significativas.
Un grupo de «control» fijo se compara con todas las demás muestras, por lo que solo debe usarse cuando tiene un grupo de control. Si no tiene un grupo de control, use la Prueba de Tukey.
Cálculo
Como Dunnett compara dos grupos, actúa de manera similar a una prueba t . La siguiente fórmula le da un valor que puede usar para comparar las diferencias de medias. La fórmula es:
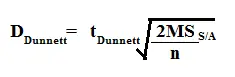
¿Necesitas ayuda? ¡Mira nuestra página de tutoría!
Paso 1: busque el valor crítico de t Dunnett en la tabla de valores críticos de Dunnett . Necesitarás:
- Su nivel alfa elegido (generalmente 5%),
- Tamaño de la muestra, n,
- Grados de libertad de la salida de ANOVA «Dentro de grupos». Esta es la «n» en la columna de la izquierda de la tabla.
Por ejemplo, supongamos que tiene un nivel alfa del 5 %, un tamaño de muestra de 5 y 20 gl. El valor crítico de Dunnett es 2,65. Ingrese el valor en la fórmula: Paso 2: encuentre los cuadrados medios (MS) del grupo dentro de la tabla fuente de ANOVA. Introduzca ese valor en la fórmula anterior. Por ejemplo, supongamos que su MS es 15,39: Paso 3: busque “n”, el número en un grupo. Para este ejemplo, eso es 5: Resolviendo la fórmula, obtenemos: D Dunnett = 2.65 * 2.481 = 6.575. 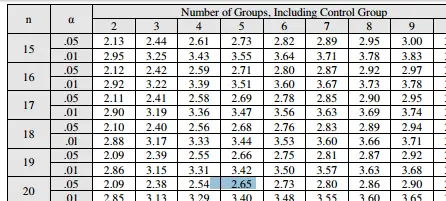
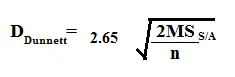
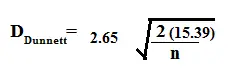
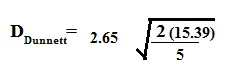
La respuesta (6.575) es la distancia crítica entre medias. Si la distancia entre la media del grupo de control y la media del grupo experimental es mayor que 6,575, entonces esa distancia es significativa. Por ejemplo, supongamos que tiene una media del grupo de control de 52 y tres medias del grupo experimental de 55, 64 y 72. Las diferencias entre las medias (valores absolutos) son:
- Grupo 1 55 – 52 = 3
- Grupo 2 64 – 52 = 12
- Grupo 3 72 – 52 = 20
Solo los grupos 2 y 3 superan la distancia de Dunnett de 6,575, por lo que son los pares significativos.
Referencias
Upton G. & Cook I. (2006.) A Dictionary of Statistics , 2ª edición, Oxford University Press, Oxford, Reino Unido.
Everitt BS & Shrondal A. (2010.) The Cambridge Dictionary of Statistics, 4.ª edición, Cambridge University Press, Cambridge, Reino Unido
Rumsey, Deborah (2009). Estadística II para Dummies . Wiley.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
