Actualizado por ultima vez el 4 de noviembre de 2021, por Luis Benites.
¿Qué es la prueba de Levene?
La prueba de Levene se usa para verificar que las varianzas sean iguales para todas las muestras cuando sus datos provienen de una distribución no normal . Puede usar la prueba de Levene para verificar la suposición de varianzas iguales antes de ejecutar una prueba como ANOVA de una vía .
Si está bastante seguro de que sus datos provienen de una distribución normal o casi normal , use la Prueba de Bartlett en su lugar.
La hipótesis nula de Levene es que las varianzas son iguales en todas las muestras. En términos más formales, eso se escribe como:
H 0 : σ 1 2 = σ 2 2 = … = σ k 2 .
La hipótesis alternativa (la que está probando) es que las varianzas no son iguales para al menos un par:
H 0 : σ 1 2 ≠ σ 2 2 ≠… ≠ σ k 2 .
La estadística de prueba es un poco fea e implica algunas sumas : Z i, j puede tener tres significados, dependiendo de si usa la media , la mediana o la media recortada de cualquier subgrupo. Las tres opciones en realidad determinan la solidez y el poder de la prueba.
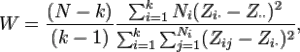
- Robustez , es una medida de qué tan bien la prueba no informa falsamente varianzas desiguales (cuando las varianzas son realmente iguales).
- La potencia es una medida de qué tan bien la prueba informa correctamente las varianzas desiguales.
Según Brown y Forsythe:
- Los medios recortados funcionan mejor con distribuciones de colas pesadas como la distribución de Cauchy .
- Para distribuciones asimétricas , o si no está seguro de la forma subyacente de la distribución, la mediana puede ser su mejor opción.
- Para distribuciones simétricas y con colas moderadas, utilice la media .
La prueba de Levene está integrada en la mayoría de los programas estadísticos. Por ejemplo, la prueba T para muestras independientes en SPSS genera una columna de «Prueba de igualdad de varianzas de Levene» como parte de la salida. El resultado de la prueba se informa como un valor p, que puede comparar con su nivel alfa para la prueba. Si el valor p es mayor que el nivel alfa , entonces puede decir que la hipótesis nula se mantiene, que las varianzas son iguales; si el valor p es más pequeño que el nivel alfa, entonces la implicación es que las varianzas no son iguales .
Ejecute una prueba de Levene para la igualdad de varianzas en SPSS
La prueba de Levene comprueba si las varianzas de dos muestras son aproximadamente iguales. Idealmente, desea un resultado no significativo para esta prueba, lo que significa que sus varianzas cumplen con la suposición de varianzas iguales. SPSS ejecutará automáticamente una prueba de Levene cada vez que ejecute una prueba t de muestras independientes, pero puede ejecutar una prueba de forma independiente siguiendo los siguientes pasos.
Mire el video para conocer los pasos detallados:
Prueba de Levene para la igualdad de varianzas SPSS 
Mira este video en YouTube .
Nota: Los siguientes pasos se ejecutan en un conjunto de datos con dos niveles de la variable independiente: en casa y en la oficina. Los puntajes de las pruebas se miden a nivel de escala.
Paso 1: Vaya a Analizar > Modelo lineal general → Univariante
Paso 2: Mueva su variable independiente a la casilla Factor fijo.
Paso 3: mueva su variable dependiente al cuadro Variable dependiente.
Paso 4: Haga clic en «Opciones», luego coloque una marca de verificación junto a Pruebas de homogeneidad. En la parte inferior, puede cambiar su nivel alfa, si lo desea. Es común establecer el nivel alfa en .01 o .001, especialmente con muestras de gran tamaño. Esto se debe a que es más probable que obtenga un resultado estadísticamente significativo para muestras más grandes.
Paso 6: Haga clic en Continuar, luego haga clic en Aceptar para ejecutar la prueba.
Lectura de la salida
Lea el resultado de la columna Sig (Basado en la media) en el cuadro Prueba de igualdad de varianzas de error de Levene. Un resultado no significativo aquí (superior a .05) indica que ha cumplido con la suposición de homogeneidad de varianza (es decir, se suponen varianzas iguales). Un resultado significativo aquí (menos de .05) indica que ha violado la suposición de homogeneidad de varianza (es decir, no se asumen varianzas iguales).
Si está leyendo el resultado como parte de una prueba t, esto le indica si debe interpretar la prueba t para varianzas iguales asumidas o no asumidas.
Referencia :
Brown, MB y Forsythe, Pruebas robustas para la igualdad de varianzas. AB (1974), Revista de la Asociación Estadounidense de Estadística, 69, págs. 364-367. Disponible aquí .
