Prueba de rango con signo de Wilcoxon: definición, cómo ejecutar, SPSS

Actualizado el 18 de febrero de 2022, por Luis Benites.

¿Qué es la prueba de rangos con signos de Wilcoxon?

La prueba de rango con signo de Wilcoxon (también llamada prueba de suma de rango con signo de Wilcoxon) es una prueba no paramétrica para comparar datos. Cuando se usa la palabra «no paramétrico» en las estadísticas, no significa que no sepa nada sobre la población. Por lo general, significa que sabe que los datos de población no tienen una distribución normal . La prueba de rango con signo de Wilcoxon se debe utilizar si las diferencias entre pares de datos no se distribuyen normalmente.

Mire el video para obtener una descripción general y cómo ejecutar la prueba de rango con signo de Wilcoxon a mano:

Prueba de rango con signo de Wilcoxon Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí

Existen dos versiones ligeramente diferentes de la prueba:

• La prueba de rango con signo de Wilcoxon compara la mediana de su muestra con una mediana hipotética.
• La prueba de rango con signo de pares emparejados de Wilcoxon calcula la diferencia entre cada conjunto de pares emparejados, luego sigue el mismo procedimiento que la prueba de rango con signo para comparar la muestra con alguna mediana.

El término «Wilcoxon» se usa a menudo para cualquiera de las dos pruebas. Por lo general, esto no es confuso, ya que debería ser obvio si los datos coinciden o no.

La hipótesis nula de esta prueba es que las medianas de dos muestras son iguales. Generalmente se utiliza:

• Como una alternativa no paramétrica a la prueba t de una muestra o la prueba t pareada .
• Para variables categóricas ordenadas (clasificadas) sin una escala numérica.

Cómo ejecutar la prueba de rango con signo de Wilcoxon en SPSS

Mire el video para aprender cómo ejecutar la prueba de Wilcoxon en SPSS:

Cómo ejecutar una prueba de rango con signo de Wilcoxon en SPSS Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí

Otra tecnología

Excel/Open Office: Descargue esta hoja de cálculo (cortesía de BioStatHandbook ).

R : Puede encontrar un código de muestra aquí en RCompanion.org .

Cómo ejecutar la prueba a mano

¿ Necesitas ayuda con las fórmulas? ¡Mira nuestra página de tutoría!

Requisitos para ejecutar la prueba de pares emparejados:

• Los datos deben coincidir.
• La variable dependiente debe ser continua (es decir, debe poder distinguir entre valores en el enésimo lugar decimal).
• No debe tener rangos empatados para obtener la máxima precisión . Si los rangos están empatados, hay una solución (ver más abajo, después del Paso 5).

Ejemplo de pregunta: ¿Hay alguna diferencia entre los valores medianos de los siguientes conjuntos de datos de tratamiento para los doce grupos?

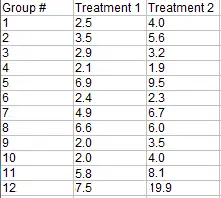
Paso 1: reste el tratamiento 2 del tratamiento 1 para obtener las diferencias: Nota : si solo tiene una muestra, calcule las diferencias entre cada variable y cero (la mediana hipotética) en lugar de la diferencia entre pares.

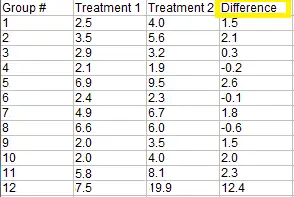
Paso 2: Coloque las diferencias en orden (columna 2 en la imagen a continuación) y luego clasifíquelas. Ignore el signo al colocar en orden de clasificación.

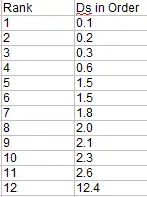
Paso 3: Haga una tercera columna y observe el signo de la diferencia (¡el que ignoró en el Paso 2!).

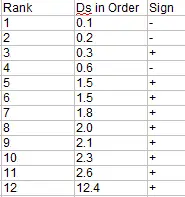
Los siguientes dos pasos calculan las sumas de rango con signo de Wilcoxon:

Paso 4: Calcular la suma de los rangos de las diferencias negativas (las que tienen signo negativo en el gráfico del Paso 3). Estás sumando los rangos aquí, no las diferencias reales:
W ^— = 1 + 2 + 4 = 7

Paso 5: Calcule la suma de los rangos de las diferencias positivas (las que tienen el signo positivo en el gráfico del Paso 3).
W ⁺ = 3 + 5,5 + 5,5 + 7 + 8 + 9 + 10 + 11 + 12 = 71

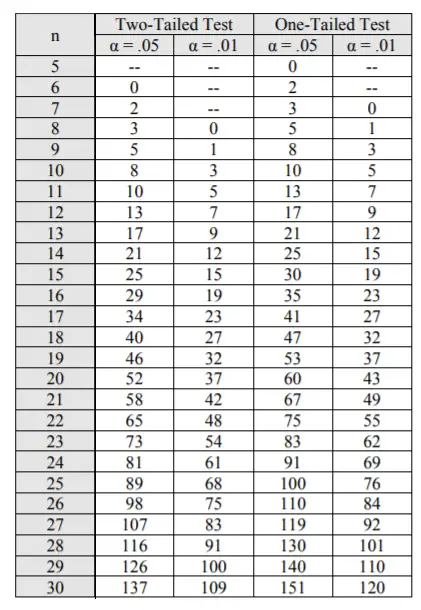
Estadística de prueba de rangos con signo de Wilcoxon y valor crítico

1. Use el menor de W ⁺ o W ^— para la estadística de prueba. Para este ejemplo, W _stat = 7.
2. Compare su estadística de prueba con un valor crítico (vea la tabla a continuación). Para este ejemplo, nuestro valor crítico para N = 12 y una prueba de dos colas (porque no se especifica la dirección) es 13 (a un nivel alfa del 5 %).

Nuestro estadístico de prueba (7) es más pequeño que el valor crítico (13), por lo que hay una diferencia significativa en las medianas. Podemos rechazar la hipótesis nula.

Referencias

Tabla: http://users.stat.ufl.edu/~winner/tables/wilcox_signrank.pdf
Breslow, N. (1970) Una prueba generalizada de Kruskal-Wallis para comparar K muestras sujetas a patrones desiguales de censura, Biometrika, 57( 3), 579–594.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Vogt, WP (2005). Diccionario de estadística y metodología: una guía no técnica para las ciencias sociales . SABIO.