Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 7 de junio de 2022, por Luis Benites.
El término “estadística V” podría referirse a cualquiera de varias estadísticas . El que esté utilizando depende del tipo de análisis que esté realizando. Por ejemplo:
- Análisis de correlación : V de Cramer
- Análisis discriminante : V de Rao
- MANOVA : V de Pillai
Estas estadísticas generalmente se denominan “V de Cramer, V de Rao y traza de Pillai respectivamente, lo que evita la confusión de terminología. Sin embargo, algunos autores usarán los términos «estadística V» sin aclaración, lo que puede resultar confuso a menos que pueda descifrar la intención del autor y el método de análisis.
Otro tipo de “estadística V” con la que te puedes encontrar es la estadística V de Von Mises, . Las estadísticas Von Mises U y V se utilizan en la teoría de la estimación, la teoría asintótica y la teoría de la probabilidad avanzada.
Las V menos comunes incluyen la V de Bhapkar, utilizada en una prueba sin distribución para la hipótesis de homogeneidad de las poblaciones c (Bhapkar & Schwarz, 1977).
1. Estadística V de Cramer
El término “estadística V” podría referirse a la estadística asociada con la correlación V de Cramer . V utilizado en este sentido es un estadístico de correlación. Te dice si dos variables covarían (cambia una variable cuando cambia la otra) y cuánto; Un valor V de 0 indica que no hay correlación, mientras que 1 indica una correlación perfecta.
2. La V de Rao
La V de Rao es una medida de la distancia entre los centroides de los grupos , lo que indica un poco acerca de la separación total de los grupos. Esta estadística en particular no le dice nada sobre el comportamiento dentro del grupo, solo el comportamiento del centroide para cada grupo.
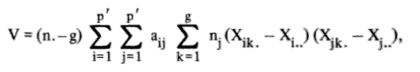
Fórmula de la V de Rao (Klecka, 1980).
3. V de Pillai
La V de Pillai (también llamada traza de Pillai-Bartlett o simplemente traza de Pillai) es una estadística MANOVA de uso general. En comparación con medidas similares (como Wilks’ Lambda o Hotelling’s Trace ), es resistente a la heterogeneidad de la varianza y también puede manejar violaciones del supuesto de normalidad (Barnes, 1993).
Referencias
Barnes, M. (1993). Oceanografía y biología marina, una revisión anual . Prensa CRC.
Bhapkar, V. y Schwarz, J. (1977). Cálculo eficiente de la V de bhapkar y puntos de significación para su uso en muestras pequeñas. Revista de Computación Estadística y Simulación. Volumen 10, 1979-Número 1.
Frey, V. (2018). La Enciclopedia SAGE de Investigación, Medición y Evaluación Educativa . Publicaciones SAGE.
IBM. Uso de la V de Rao como criterio en el análisis discriminante por pasos en SPSS Statistics.
Klecka, W. Análisis Discriminante, Volumen 19; Volumen 1980. SABIO, 1980.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
