Actualizado por ultima vez el 13 de noviembre de 2021, por Luis Benites.
Haga clic aquí si desea encontrar el coeficiente de asimetría de Pearson en Excel.
Mira el video para ver un ejemplo:
Cálculo del coeficiente de asimetría de Pearson Mira este video en YouTube . ¿mira el video? Haga clic aquí
¿Qué es el coeficiente de asimetría de Pearson?
Karl Pearson desarrolló dos métodos para encontrar la asimetría en una muestra .
- El coeficiente de asimetría #1 de Pearson usa el modo . La fórmula es: Donde = la media , Mo = la moda y s = la desviación estándar de la muestra. Consulte : asimetría del modo de Pearson .
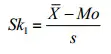
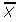
- El coeficiente de asimetría n.° 2 de Pearson utiliza la mediana . La fórmula es: Donde = la media, Mo = la moda y s = la desviación estándar de la muestra. Generalmente se usa cuando no conoces el modo.
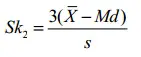
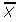
Problema de ejemplo: utilice el coeficiente n.° 1 y n.° 2 de Pearson para encontrar la asimetría de los datos con las siguientes características:
- Media = 70,5.
- Mediana = 80.
- Moda = 85.
- Desviación estándar = 19,33.
Coeficiente de asimetría #1 de Pearson (moda) :
Paso 1: Restar la moda de la media: 70,5 – 85 = -14,5.
Paso 2: Divida por la desviación estándar: -14,5 / 19,33 = -0,75.
Coeficiente de asimetría de Pearson n.° 2 (mediana) :
Paso 1: reste la mediana de la media: 70,5 – 80 = -9,5.
Paso 2: Multiplique el Paso 1 por 3: -9.5(3) = -28.5
Paso 2: Divida por la desviación estándar: -28.5 / 19.33 = -1.47.
Precaución : el primer coeficiente de asimetría de Pearson utiliza la moda. Por lo tanto, si la moda se compone de muy pocos datos, no será una medida estable de tendencia central. Por ejemplo, la moda en ambos conjuntos de datos es 9:
1 2 3 4 5 6 7 8 9 9.
1 2 3 4 5 6 7 8 9 9 9 9 9 9 9 9 9 9 9 9 10 12 12 13.
En el primer conjunto de datos, la moda solo aparece dos veces. Esta no es una buena medida de tendencia central, por lo que se le advierte que no utilice el coeficiente de asimetría de Pearson. El segundo conjunto de datos tiene un conjunto más estable (la moda aparece 12 veces). Por lo tanto, el coeficiente de asimetría de Pearson probablemente le dará un resultado razonable.
Interpretación
En general:
- La dirección de la asimetría viene dada por el signo.
- El coeficiente compara la distribución de la muestra con una distribución normal. Cuanto mayor sea el valor, mayor será la diferencia entre la distribución y la distribución normal.
- Un valor de cero significa que no hay sesgo en absoluto.
- Un valor negativo grande significa que la distribución tiene un sesgo negativo.
- Un valor positivo grande significa que la distribución tiene un sesgo positivo.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Lindström, D. (2010). Schaum’s Easy Outline of Statistics , segunda edición (Schaum’s Easy Outlines) 2ª edición. Educación McGraw-Hill
“Cook, T. (2005). Introducción a los métodos estadísticos para ensayos clínicos (Chapman & Hall/CRC Texts in Statistical Science) 1ª edición. Chapman y Hall/CRC

