Actualizado por ultima vez el 3 de diciembre de 2021, por Luis Benites.
Es posible que desee leer este artículo primero: ¿Qué es un factorial (!)?
El coeficiente multinomial , utilizado en combinatoria , es una extensión del coeficiente binomial . Se usa para encontrar permutaciones cuando tiene valores repetidos o elementos duplicados. La fórmula es: En términos formales, la fórmula del coeficiente multinomial da la expansión de (k 1 + k 2 … + k n ) donde k i son números enteros no negativos . De manera informal, puede considerarlo como una forma de encontrar cuántas permutaciones son posibles cuando tiene valores duplicados para k . Esto se ilustra mejor con un ejemplo.
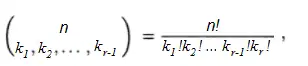
Ejemplo de coeficiente multinomial
Harris et . al en Combinatoria y Teoría de grafos . Digamos que desea contar el número de formas de ordenar n objetos. Si los objetos son todos diferentes, ¡entonces hay n! formas de ordenarlos. Pero si algunos de los objetos son un conjunto múltiple y algunos de los objetos son iguales, n! producirá demasiadas permutaciones .
Por ejemplo, supongamos que está tratando de encontrar el número de permutaciones diferentes para las letras de la palabra Mississippi . Tenga en cuenta que en realidad solo hay cuatro letras únicas: MISP. El número de veces que aparecen las letras:
- METRO = 1
- yo = 4
- S = 4
- PAG = 2
Insertando esos valores en la fórmula del coeficiente multinomial, donde n es el número total de letras en la palabra MISSISSIPPI, y k n es el número de letras individuales (de la lista anterior):
n! / k 1 ! * k 2 ! * k 3 ! * k 4 ! = 11! / ( 1! * 4! * 4! * 2! ) = 11! / ( 1 * 24 * 24 * 2 ) = 34 650.
Tenga en cuenta que n! da 11! = 39916800, que es mucho mayor que el número real de permutaciones distinguibles.
Entonces, puede pensar en el coeficiente multinomial como una «corrección de permutaciones» cuando hay elementos duplicados en el conjunto de conteo.
Referencias:
John Harris, Jeffry L. Hirst, Michael Mossinghoff. Combinatoria y Teoría de Grafos.
.
