Contenido de este artículo
Actualizado el 2 de enero de 2022, por Luis Benites.
1. ¿Qué es un juego múltiple?
Un conjunto múltiple en matemáticas es una generalización del concepto de conjunto. Es una colección de números desordenados (u otros elementos), donde cada elemento x aparece un número finito de veces.
La diferencia entre conjuntos y multiconjuntos está en cómo abordan los múltiplos: un conjunto incluye cualquier número como máximo una vez, mientras que un conjunto múltiple permite varias instancias del mismo número. Solo hay un conjunto con los elementos a y b , el conjunto {a,b}, pero hay muchos multiconjuntos: {a, b, b}, {a, a, b} y {a, a, a, a , b, b} son solo algunos.
El número de multiconjuntos k largos usando n símbolos se llama n multichoose k , y se escribe como
![]() Esto se puede escribir en términos del coeficiente binomial :
Esto se puede escribir en términos del coeficiente binomial :
![]()
Multiplicidad
La multiplicidad de un elemento x en un conjunto múltiple es solo el número de veces que ese elemento aparece en el conjunto. Por ejemplo, en el multiconjunto {3, 3, 4, 5, 6} el elemento 3 tiene multiplicidad 2. Los elementos 4, 5 y 6 tienen todos multiplicidad 1.
Si conocemos los elementos incluidos y la multiplicidad de cada uno de ellos sabemos todo sobre un multiconjunto. Un conjunto múltiple que incluye solo 4 con multiplicidad 2, 5 con multiplicidad 7 y 99 con multiplicidad 2 se puede escribir como {4, 4, 5, 5, 5, 5, 5, 99, 99}. El orden no importa, así que esto es lo mismo que {4, 99, 5, 4, 99, 5, 5, 5, 5}
El juego múltiple en uso
Los conjuntos múltiples son importantes tanto en matemáticas como en informática. Nos ayudan a realizar un seguimiento de los elementos en las bases de datos y son la columna vertebral de la combinatoria moderna .
Un ejemplo de multiconjuntos es una lista de los factores primos de un número. Los factores de 4 son {2,2}, y esto es diferente a los factores primos de 2,{2}. Los factores primos de 90, {3,3,5,2}, son diferentes a los factores primos de 30: {3,5,2}
2. ¿Qué es Multiopción?
Multichoose es una forma de elegir elementos, donde n es el número de elementos para elegir yk es el conjunto de elementos para elegir. Por ejemplo, 10 multichoose 4 es el número de formas posibles de elegir un conjunto de 4 elementos de un grupo de 10 elementos diferentes. Más técnicamente, es el número de multiconjuntos k largos, formados por n símbolos. El orden no es importante y se permiten repeticiones.
Por ejemplo, 4 multiescoja 2 es igual a 10, porque el número posible de conjuntos múltiples de dos elementos para cuatro elementos {j, k, l, m} son {j, j}, {j, k}, {j, l}, { j, m}, {k, k}, {k, l}, {k, m}, {l, l}, {l, m} y {m, m}.
Encontrar n multiselección k
Para conjuntos pequeños, la forma más fácil es hacer una lista de todas las posibilidades. Por ejemplo: ¿Está preguntando «cuántos conjuntos múltiples del valor superior (2 elementos de largo) se pueden encontrar del valor inferior (el conjunto {1,2})»? La solución es 3: {1,1}, {1,2}, {2,2}.
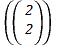
También se pueden encontrar soluciones a problemas de selección múltiple justificando las columnas del triángulo de Pascal y moviendo los números hacia arriba (Isaak, 2016; Bailer-Jones, 2017):
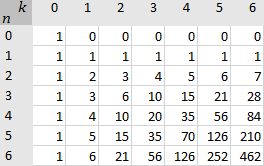
Las primeras soluciones {n,k} como se encuentran en el triángulo de Pascal.
Comparación con el coeficiente binomial
Escribimos el coeficiente de elección múltiple con doble paréntesis:
![]() . Puede notar que esta ecuación es similar al coeficiente binomial : los dos son muy similares. Las definiciones de los dos coeficientes (de Arthur et. al, 2003) son:
. Puede notar que esta ecuación es similar al coeficiente binomial : los dos son muy similares. Las definiciones de los dos coeficientes (de Arthur et. al, 2003) son:
![]()
- Coeficiente binomial : el número de subconjuntos de elementos k de {1,…,n}
- Coeficiente de elección múltiple: el número de subconjuntos múltiples de elementos k de {1,…,n}.
El coeficiente binomial nos dice el número de formas en que podemos elegir k resultados desordenados de n posibilidades. No se permiten repeticiones en el coeficiente binomial; cada una de las n posibilidades solo se puede elegir una vez. En multichoose se permiten repeticiones : podemos elegir varias veces de una misma posibilidad.
Estrellas y Barras
A veces, los problemas de selección múltiple se denominan problemas de estrellas y barras. Esto se debe a que una forma de resolverlos consiste en imaginar que nuestros k elementos son k estrellas y tenemos n – 1 puntos límite que separan los tipos. La forma en que se colocan las estrellas y los puntos límite definen el problema.
Por ejemplo, en nuestro problema de la tienda de dulces tenemos 4 – 1 = tres barras ||| separando los tipos (es decir, 1|2|3|4). Dado que el orden no importa en los problemas de selección múltiple, podemos ordenar nuestras selecciones de dulces de cualquier manera que sea conveniente para realizar un seguimiento de ellos. Esto implica tener siempre los mismos artículos en el mismo orden. Aquí podríamos marcar primero cualquier regaliz elegido, luego gotas de menta, luego gotas de limón y finalmente trufas. En orden, esos son:
- Regaliz
- Menta
- Limón
- Trufas
Entonces, si solo elegimos un regaliz, podemos escribirlo como ☆|||.
Si solo elegimos una gota de menta, haz que |☆||.
Solo unas gotas de limón serían ||☆|,
y solo una trufa |||☆.
Un regaliz y una trufa se escribirían ☆|||☆.
Ejemplo de pregunta (Benjamin & Quinn, 2003): Use estrellas y barras para representar la siguiente distribución de 10 dulces a 4 niños:
- El niño 1 recibe 4 dulces,
- El niño 2 recibe 5 dulces,
- El niño 3 recibe 0 dulces,
- El niño 4 recibe 1 caramelo.
Solución :
☆☆☆☆|☆☆☆☆☆||☆
Referencias
Isaac (2016). Inferencia práctica bayesiana. Prensa de la Universidad de Cambridge.
Bailer-Jones (2017). Elija Multiopción. 47th SEICCGTC en FAU, marzo de 2016. Recuperado el 8 de octubre de 2016 de: http://www.lehigh.edu/~gi02/Boca16b.pdf
Benjamin & Quinn (2003). Pruebas que realmente cuentan: el arte de la prueba combinatoria . MAA.
