Contenido de este artículo
Actualizado el 27 de agosto de 2021, por Luis Benites.
La complejidad de Kolmogorov y el principio de longitud mínima de descripción (MDL) lo ayudan a elegir entre modelos alternativos. La selección de modelos es un gran desafío en estadística, y MDL brinda una solución genérica al comprimir datos. La idea básica es que el modelo óptimo es el modelo más comprimido . Kolmogorov Complexity lo ayuda a elegir un modelo fomentando una hipótesis simple para explicar los datos.
Estrechamente relacionado con la navaja de Occam , MDL establece que la mejor explicación para un conjunto de datos es aquella que le permite comprimir los datos tanto como sea posible; para codificarlo de la manera más corta. Cuanto más se puede comprimir un conjunto de datos, más regularidades aparecen y más se puede aprender de los datos.
Complejidad de Kolmogorov
“…dados algunos datos, es preferible la hipótesis más simple que los explique.” ~Rissanen (1989)
Con MDL, la complejidad de Kolmogorov se usa para encontrar la hipótesis «más simple» . La complejidad de Kolmogorov es el código más corto que haría que una máquina de Turing imprimiera un conjunto de números. Por ejemplo, el siguiente diagrama de dispersión muestra una serie de coordenadas: Estos puntos se pueden describir de varias maneras que involucran ecuaciones lineales y listas de puntos de coordenadas en un plano cartesiano . Sin embargo, la forma más corta de describir los puntos es:
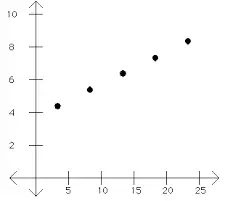
- La coordenada del primer punto,
- La dirección de la línea,
- Distancia entre puntos,
- Número total de puntos.
El «código» anterior es, por lo tanto, la complejidad de Kolmogorov para la serie de puntos anterior.
En un mundo ideal, podríamos usar el principio de longitud de descripción mínima para elegir un modelo usando la Complejidad de Kolmogorov. Comparando estos códigos más cortos para diferentes modelos, sería fácil ver cuál era el más corto absoluto ; en MDL ideal se elegiría este modelo.
Esto funciona teóricamente porque no importa qué lenguaje informático (de propósito general) se use: las longitudes de los programas más cortos impresos solo diferirán en una constante, por lo que las diferencias entre programas para varios modelos son estables.
Solo hay un problema con este método : la complejidad de Kolmogorov, si bien sería increíblemente útil si pudiéramos obtener una calculadora para escupirla, no es computable. No hay ningún programa de computadora de uso general o, teóricamente, ninguna posibilidad de escribir uno, que encuentre el programa más corto que imprima A para cualquier conjunto de datos o modelo A.
Práctico Mínimo Descripción Longitud Teoría
Dado que no podemos hacer lo que nos gustaría hacer (resumir los resultados de cada modelo en el ‘código más breve posible’ y ver cuál es más breve), necesitamos trabajar con lo que podamos. En lugar de utilizar lenguajes informáticos de propósito general, utilizamos métodos más específicos para resumir nuestros modelos; Usamos lenguajes específicos que, si bien no pueden describir nada, al menos describen nuestros modelos. Podemos usar distribuciones de probabilidad para describir nuestros datos y modelos de regresión lineal para determinar qué se ajusta mejor.
Referencias
Grunwald, Peter D. El principio de longitud mínima de descripción, Capítulo 1. Obtenido de http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.159.403&rep=rep1&type=pdf el 26 de abril de 2018
Singh, Aarti. 10-704 Procesamiento de información y aprendizaje Notas de clase: Clase 13: Longitud mínima de descripción. Recuperado de http://www.cs.cmu.edu/~aarti/Class/10704/lec13-MDL.pdf el 26 de abril de 2018
Hansen, Mark H., Yu, Bin. Selección del modelo y principio de longitud mínima de descripción.
Recuperado de https://www.stat.berkeley.edu/~binyu/summer08/mdlrevew1.pdf el 27 de abril de 2018
Rissanen, J. (1989). Complejidad estocástica en la consulta estadística . Científico Mundial.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
