Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 28 de noviembre de 2021, por Luis Benites.
¿Qué es una diferencia de medias (DM)?
La diferencia de medias, o diferencia de medias, mide la diferencia absoluta entre el valor medio en dos grupos diferentes. En los ensayos clínicos, te da una idea de cuánta diferencia hay entre los promedios del grupo experimental y los grupos de control.
Nota : aunque muchos autores usan el término diferencia de medias, tiene más sentido intuitivo decir diferencia entre medias . Eso es porque en realidad no estás calculando ningún medio; Ya tendrá dos o más medios, y todo lo que necesita hacer es encontrar una diferencia entre ellos. En otras palabras, estás encontrando una diferencia entre medias y no una media de diferencias.
¿Por qué “Diferencias absolutas”?
La definición requiere encontrar la diferencia absoluta entre dos elementos.
En matemáticas, una diferencia es una resta . Por ejemplo, la diferencia entre 10 y 2 es 8 (10 – 2 = 8). Sin embargo, te encuentras con problemas con los números negativos. Por ejemplo, la diferencia entre -1 y 1 es: -1 – 1 = -2. En términos de la vida real, una diferencia o distancia tiene más sentido si es un valor positivo, por lo que tomamos el valor absoluto de la diferencia : |-2| = 2
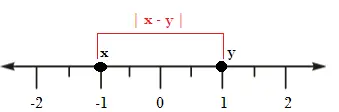
La distancia entre -1 y 1 en una recta numérica es 2 (contando las unidades de -1 a 1).
Diferencia de medias estandarizada
A veces querrás comparar medias entre grupos, pero no puedes porque tienen unidades de medida diferentes. Por ejemplo, los estudios que miden la depresión pueden usar diferentes escalas de calificación de la depresión . La diferencia de medias estandarizada (DME) es una forma de medir el tamaño del efecto ; estandariza los resultados de las pruebas para que puedan compararse. Por ejemplo, una SMD de 0,60 basada en los resultados A de un estudio es igual a una SMD de 0,60 calculada en el mismo resultado A en un estudio separado (las SMD generalmente se redondean a dos decimales).
La fórmula general es:
SMD = Diferencia en el resultado medio entre grupos / Desviación estándar del resultado entre los participantes
Sin embargo, la fórmula difiere ligeramente según la estadística SMD que utilice. Por ejemplo, la versión D de Cohen usa una desviación estándar agrupada, mientras que la versión g de Hedges usa una desviación estándar ponderada y agrupada.
Diferencia media hipotética
La diferencia media hipotética surge en programas como Excel, cuando ejecuta ciertas pruebas (como una prueba t ). Básicamente, le está diciendo al programa lo que hay en sus declaraciones de hipótesis, por lo que debe conocer su hipótesis nula . Por ejemplo, supongamos que tiene las siguientes declaraciones de hipótesis:
- Hipótesis Nula: M1 – M2 = 10
- Hipótesis alternativa: M1 – M2 ≠ 10
Pondrás 10 en el cuadro de diferencia de medias hipotética, porque eso es lo que establece tu hipótesis nula. Si tiene la hipótesis de que no hay diferencia, ingrese 0.
Excel no permite valores negativos aquí, así que si sospecha que hay una diferencia negativa, cambie sus variables (para que en realidad esté probando una diferencia positiva ).
Distribución muestral de la diferencia entre medias
La distribución muestral de la diferencia entre medias son todas las posibles diferencias que puede tener un conjunto de dos medias. La fórmula para la media de la distribución muestral de la diferencia entre medias es:
Por ejemplo, supongamos que la puntuación media en una prueba de depresión para un grupo de 100 hombres de mediana edad es 35 y para 100 mujeres de mediana edad es 25. Si tomó una gran cantidad de muestras de ambos grupos y calculó la media diferencias, la media de todas las diferencias entre todas las medias de la muestra sería 35 – 25 = 10.
Prueba de diferencias entre medias
Por sí sola, la diferencia de medias no te dice mucho (aparte de darte un número para la diferencia). El número puede ser estadísticamente significativo , o simplemente podría deberse a variaciones aleatorias o al azar. Para probar la hipótesis de que sus resultados podrían ser significativos, ejecute una prueba de hipótesis para las diferencias entre las medias.
Para comparar dos medias independientes , ejecute una prueba t de dos muestras . Esta prueba supone que las varianzas de ambas muestras son iguales. Si no lo son, ejecute la prueba de Welch para varianzas desiguales .
Para muestras dependientes (es decir, muestras que están conectadas de alguna manera) ejecute una prueba t de muestras pareadas.
Referencias
Agresti A. (1990) Análisis de datos categóricos. John Wiley and Sons, Nueva York.
Gonick, L. (1993). La guía de dibujos animados de estadísticas . Harper Perennial.
Klein, G. (2013). La caricatura Introducción a la estadística. Colina y Wamg.
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Prensa Pearson FT
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
