Actualizado por ultima vez el 19 de febrero de 2022, por Luis Benites.
La distribución de arcoseno y la distribución de arcoseno generalizada se encuentran en el estudio de la fluctuación de la caminata aleatoria , la teoría de la renovación y como el anterior de Jeffrey para los éxitos en una prueba de Bernoulli . La distribución arcoseno generalizada , utilizada en estadística matemática, es un caso especial de la distribución beta I , cuando a = b = ½.
Se llama distribución de arcoseno porque “arcosen x” es el arco que tiene un seno de x.
Aunque la distribución se usa en algunas áreas matemáticas bastante importantes, un ejemplo simple de para qué se puede usar la distribución es la fracción de tiempo que un jugador puede ganar en un juego de lanzamiento de monedas, suponiendo que las monedas tengan un peso justo (Rasnick, 2019).
PDF para la distribución Arcsine
La función de densidad de probabilidad (PDF) de la distribución de arcoseno estándar se define como: La PDF se admite para un intervalo de entre 0 y 1 (0 < 1). Fuera de este límite, la densidad es cero. La distribución se puede generalizar para incluir cualquier soporte delimitado entre dos valores ayb , o mediante el uso de parámetros de escala y parámetros de ubicación .
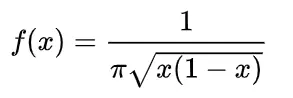
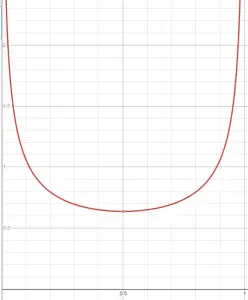
La PDF de la distribución del arcoseno tiene forma de U :
CDF para la distribución Arcsine
La función de distribución acumulada (CDF) para la función arcsen es: La CDF es válida para valores de x de 0 a 1 (0 < x < 1); La CDF se concentra cerca de los valores límite 0 y 1. A medida que la distribución se acerca mucho a 1, tiende a infinito . Incluye el seno inverso (arcsin) , que es donde la distribución recibe su nombre.
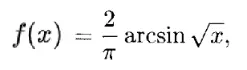
Referencias
Agrawal, N. et al. Distribución Arcsen. Recuperado el 21 de enero de 2020 de: https://www.boost.org/doc/libs/1_58_0/libs/math/doc/html/math_toolkit/dist_ref/dists/arcine_dist.html
Balakrishnan, N. & Nevzorov, V. ( 2004). Una cartilla sobre distribuciones estadísticas . John Wiley & Sons.
Hazewinkel, M. (1994). Enciclopedia de Matemáticas (conjunto). Springer Science & Business Media.
Mörters, P. & Peres, Y. (2010). Movimiento browniano. Prensa de la Universidad de Cambridge.
Equipo central de distribuciones de R-forge. (2009-2010). Manual sobre distribuciones de probabilidad. Recuperado el 21 de enero de 2020 de: http://www.stat.rice.edu/~dobelman/textfiles/distributions.r-forge.pdf
Rasnick, Rebecca, «Generalizaciones de la distribución Arcsine» (2019). Tesis y disertaciones electrónicas. Documento 3565. https://dc.etsu.edu/etd/3565

