Actualizado por ultima vez el 7 de enero de 2022, por Luis Benites.
¿Qué es una distribución de Bernoulli?
Una distribución de Bernoulli es una distribución de probabilidad discreta para un ensayo de Bernoulli , un experimento aleatorio que tiene solo dos resultados (generalmente llamado «Éxito» o «Fracaso»). Por ejemplo, la probabilidad de obtener cara (un «éxito») al lanzar una moneda es de 0,5. La probabilidad de “fracaso” es 1 – P (1 menos la probabilidad de éxito, que también es igual a 0,5 para el lanzamiento de una moneda). Es un caso especial de la distribución binomial para n = 1. En otras palabras, es una distribución binomial con un solo intento (por ejemplo, un lanzamiento de una sola moneda).
Mire el video para ver la definición y cómo encontrar el PDF, la varianza, el valor esperado y las probabilidades:
Probabilidad de distribución de Bernoulli y PDF 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
La probabilidad de falla se etiqueta en el eje x como 0 y el éxito se etiqueta como 1. En la siguiente distribución de Bernoulli, la probabilidad de éxito (1) es 0.4 y la probabilidad de falla (0) es 0.6: La probabilidad función de densidad (pdf) para esta distribución es p x (1 – p) 1 – x , que también se puede escribir como:
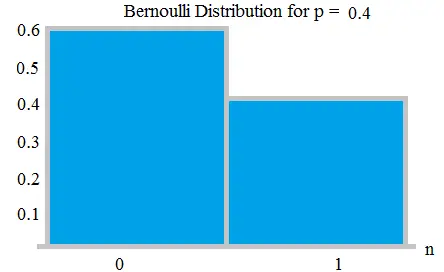
El valor esperado de una variable aleatoria , X, para una distribución de Bernoulli es:
E[X] = p.
Por ejemplo, si p = 0,04, entonces E[X] = 0,04.
La varianza de una variable aleatoria de Bernoulli es:
Var[X] = p(1 – p).
¿Qué es un ensayo de Bernoulli?
Una prueba de Bernoulli es uno de los experimentos más simples que puede realizar. Es un experimento en el que puedes tener uno de dos resultados posibles. Por ejemplo, «Sí» y «No» o «Cara» y «Cruz». Algunos ejemplos:
- Lanzamientos de monedas : registre cuántas monedas caen cara y cuántas caen cruz.
- Nacimientos : cuántos niños nacen y cuántas niñas nacen cada día.
- Rolling Dice : la probabilidad de que una tirada de dos dados resulte en un doble seis.
El lanzamiento de monedas como un juego de probabilidad y azar ha existido desde la época romana.
Los juicios de Bernoulli generalmente se expresan en términos de éxito y fracaso . El éxito no significa éxito de la manera habitual, simplemente se refiere a un resultado del que desea realizar un seguimiento. Por ejemplo, es posible que desee averiguar cuántos niños nacen cada día, por lo que llama al nacimiento de un niño un «éxito» y al nacimiento de una niña un «fracaso». En el ejemplo de lanzamiento de dados, una tirada de dado doble seis sería su «éxito» y todo lo demás tirado se consideraría un «fracaso».
Independencia
Una parte importante de cada prueba de Bernoulli es que cada acción debe ser independiente . Eso significa que las probabilidades deben permanecer iguales a lo largo de las pruebas; cada evento debe estar completamente separado y no tener nada que ver con el evento anterior.
Ganar un raspadito de lotería es un evento independiente . Sus probabilidades de ganar con un boleto son las mismas que con cualquier otro boleto. Por otro lado, sacar números de lotería es un evento dependiente. Los números de lotería salen de una bola (los números no se reemplazan), por lo que la probabilidad de que se elijan números sucesivos depende de cuántas bolas queden; cuando hay cien bolas, la probabilidad de que salga cualquier número es de 1/100, pero cuando solo quedan diez bolas, la probabilidad se dispara hasta 1/10. Si bien es posible encontrar esas probabilidades, no es una prueba de Bernoulli porque los eventos (elegir los números) están conectados entre sí.
El proceso de Bernoulli conduce a varias distribuciones de probabilidad:
La distribución de Bernoulli está estrechamente relacionada con la distribución Binomial. Siempre que cada prueba individual de Bernoulli sea independiente, el número de éxitos en una serie de pruebas de Bernoulli tiene una distribución binomial. La distribución de Bernoulli también se puede definir como la distribución Binomial con n = 1.
Uso de la Distribución de Bernoulli en Epidemiología
En experimentos y ensayos clínicos, la distribución de Bernoulli a veces se usa para modelar un solo individuo que experimenta un evento como la muerte, una enfermedad o la exposición a una enfermedad. El modelo es un excelente indicador de la probabilidad de que una persona tenga el evento en cuestión.
- 1 = “evento” (P = p)
- 0 = “sin evento” (P = 1 – p)
Las distribuciones de Bernoulli se utilizan en la regresión logística para modelar la aparición de enfermedades.
Referencias
Evans, M.; Hastings, N.; y Peacock, B. “Bernoulli Distribution”. cap. 4 en Distribuciones estadísticas, 3ª ed . Nueva York: Wiley, págs. 31-33, 2000.
WSU. Recuperado el 15 de febrero de 2016 de: www.stat.washington.edu/peter/341/Hypergeometric%20and%20binomial.pdf
