Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 12 de enero de 2022, por Luis Benites.
Distribución de energía estándar
La distribución de potencia estándar tiene la función de densidad de probabilidad f(x) = Βx Β-1 ; 0 < x < 1.
La distribución tiene un parámetro de forma , Β.
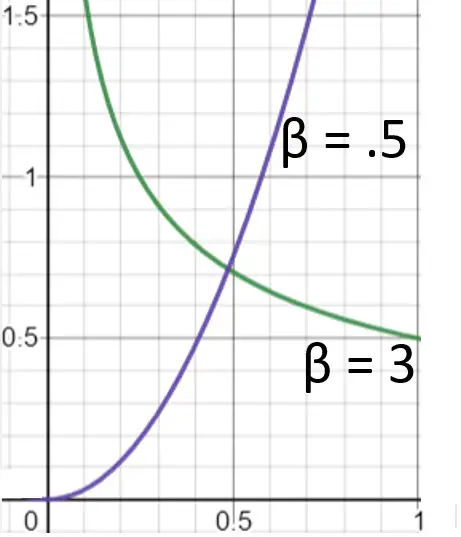
Gráfico de la distribución de potencia estándar con dos valores para el parámetro de forma, Β.
La distribución no se encuentra muy a menudo en la literatura, posiblemente porque no es un modelo realista para aplicaciones del mundo real. Una aplicación es la generación de números aleatorios, donde se extraen muestras aleatorias de la función [1].
Distribución de energía U
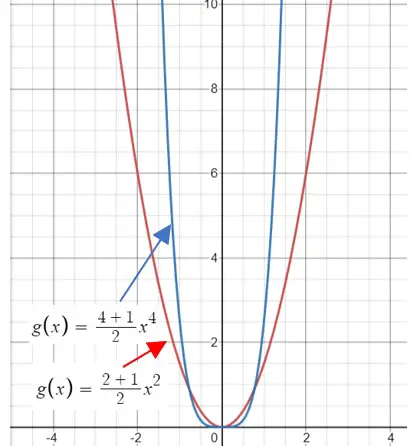
Gráfico de la distribución de potencia U con k = 1 (rojo) y k = 2 (azul).
La distribución de potencia U estándar es una distribución de probabilidad continua en forma de U con un parámetro de forma k &is en ℕ. La distribución, que se define en el intervalo [-1, 1], se basa en una familia de funciones de potencia que adoptan la distintiva forma de u [2].
La distribución de potencia U tiene la función de densidad de probabilidad: . En general, la PDF es monótona y creciente, con un máximo global en el límite superior del dominio (x = 1 para la distribución estándar). El parámetro de forma controla la forma general, incluida la altura, la extensión y la ubicación de su punto máximo. Cuando k = 1 (graficado en rojo en la imagen de arriba), la distribución se llama distribución U-cuadrática . Cuando k = 0, la distribución se reduce a la distribución uniforme, que no tiene forma de u.
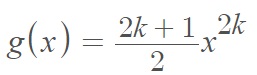
La función de distribución tiene algunas propiedades notables:
- simetría sobre x = 0,
- Cóncavo hacia arriba (es decir, una U con el lado derecho hacia arriba),
- Modos en x = ±1,
- Decreciente para x < 0 y creciente para x>0.
- Mínimo en x = 0.
Artículo relacionado : Distribución de Potencia Exponencial .
Referencias
Gráfico creado con Desmos .
[1] numpy.random.power .
[2] Siegrist, K. 5.26: La distribución U Power. Recuperado el 31 de diciembre de 2021 de: https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_(Siegrist)/05%3A_Special_Distributions/5.26%3A_The_U-Power_Distribution
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
