Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 29 de enero de 2022, por Luis Benites.
¿Qué es la distribución de Rayleigh?
La distribución de Rayleigh es una distribución de probabilidad continua que lleva el nombre del inglés Lord Rayleigh . Es un caso especial de la distribución Weibull con un parámetro de escala de 2. Cuando se establece un Rayleigh con un parámetro de forma (σ) de 1, es igual a una distribución chi cuadrada con 2 grados de libertad .
La notación X Rayleigh(σ) significa que la variable aleatoria X tiene una distribución Rayleigh con parámetro de forma σ. La función de densidad de probabilidad (X > 0) es: Donde e es el número de Euler .
A medida que aumenta el parámetro de forma, la distribución se vuelve más ancha y plana.
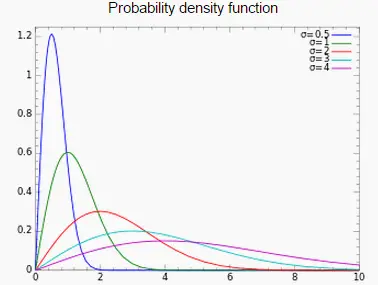
distrito de Rayleigh mostrando varios parámetros de forma diferentes, σ.
La distribución es muy utilizada:
- En la teoría de las comunicaciones, para modelar múltiples caminos de señales dispersas densas que llegan a un receptor.
- En las ciencias físicas para modelar la velocidad del viento, la altura de las olas y la radiación de sonido/luz.
- En ingeniería, para medir la vida útil de un objeto, donde la vida útil depende de la edad del objeto. Por ejemplo: resistencias, transformadores y condensadores en equipos de radar de aviones. 1
- En la ciencia de la imagen médica, para modelar la variación del ruido en la resonancia magnética.
Varianza y media (valor esperado) de una distribución de Rayleigh
El valor esperado (la media ) de Rayleigh es: La forma en que se deriva esta ecuación implica resolver una integral , usando cálculo : El valor esperado de una distribución de probabilidad es: E(x) = ∫ xf(x)dx.
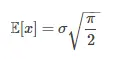
Sustituyendo en la función de densidad de probabilidad de Rayleigh, esta se convierte en la integral impropia : Donde:
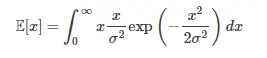
- exp es la función exponencial ,
- dx es el operador diferencial .
Resolver la integral por usted da el valor esperado de Rayleigh de σ √(π/2)
La varianza de una distribución de Rayleigh se obtiene de manera similar, dando la fórmula de varianza de:
Var(x) = σ 2 ((4 – π)/2).
Referencias
:
Una mezcla de 3 componentes: propiedades y estimación en el marco bayesiano. Aslam et. Alabama. Consultado el 3 de octubre de 2015. Disponible aquí .
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
