Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 25 de diciembre de 2021, por Luis Benites.
¿Qué es una distribución degenerada?
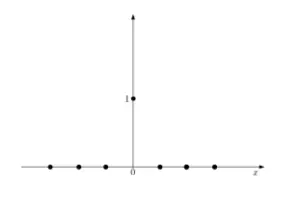
Una distribución degenerada con c = 0.
Una distribución degenerada (a veces llamada distribución constante ) es una distribución de una variable aleatoria degenerada, una constante con probabilidad de 1. En otras palabras, una variable aleatoria X tiene un único valor posible.
Algunos ejemplos:
- Un dado ponderado (o uno que tiene un número 6 en todas las caras) siempre cae en el número seis, por lo que la probabilidad de un seis (P(6)) es 1.
- Una moneda tiene dos caras y dos caras (existen miles de estas «monedas mágicas», pero también las hay reales. Ver: 1859 Céntimo de cabeza india de dos caras para ver un ejemplo).
- (Cálculo): Una variable aleatoria X que se distribuye como la derivada de k cuando k=1. Como k=1, la distribución solo puede tener un valor de 0 (porque la derivada de cualquier constante es 0).
Como no hay dispersión de variables alrededor de la media , la varianza de la distribución degenerada es cero (Var(X) = 0).
Más definiciones formales
La definición formal de una variable aleatoria degenerada es que es una distribución que asigna toda la probabilidad a un solo punto:
Una variable aleatoria, X, es degenerada si, para alguna constante, c, P(X = c) = 1
Si una variable aleatoria no cumple con la definición anterior, entonces no es degenerada.
Una distribución degenerada tiene un único parámetro, c, donde -∞ < c < ∞. La definición formal es:
para algunos una constante, x, F(x) =
- 0, para x < c,
- 1, para x ≥ c.
Una distribución no degenerada es aquella que no cumple con esta definición.
Usar
Las distribuciones degeneradas generalmente se enseñan en cursos de estadística avanzada como estadística matemática. Se pueden definir como casos especiales de la distribución binomial , normal y geométrica, entre otras, y se utilizan a menudo en la teoría de colas donde los tiempos de servicio o los tiempos entre llegadas de los sistemas son constantes.
Referencia :
V. Sundarapandian. Probabilidad, Estadística y Teoría de Colas. 1 de diciembre de 2009
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
