Actualizado por ultima vez el 31 de agosto de 2021, por Luis Benites.
¿Qué es la distribución de Gompertz?
La distribución de Gompertz , llamada así por Benjamin Gompertz , es una distribución de probabilidad continua exponencialmente creciente. Es básicamente una distribución de valor extremo truncada (Johnson et. al, 1994). Por lo tanto, también se denomina EVD Tipo I. Aunque el rango teórico es de cero a infinito positivo , la mayoría de las aplicaciones de esta distribución son para tasas de mortalidad humana con un rango de 0 a ≅ 100. También se usa en otros campos, incluidos biología y demografía.
Función de densidad de probabilidad
Dos parámetros de forma , δ y κ controlan la forma de la función de densidad de probabilidad .
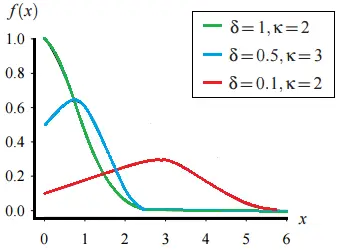
Distribución de Gompertz que muestra varios valores para los parámetros de forma delta y kappa.
Definicion formal
El Gompertz se puede definir mediante la siguiente ecuación diferencial (Marshall & Olkin, 2007): Donde :
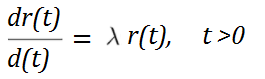
- r(t) es la tasa de riesgo
Cuando λ = 1, se convierte en la distribución exponencial.
Gompertz supuso que la tasa de riesgo eran tus posibilidades de morir en el tiempo t . Concluyó que esta tasa aumentaba en progresión geométrica : cuando λ y ξ son ambos menores que cero, esto se convierte en la distribución negativa de Gompertz.
Relación con otras distribuciones
El Gompertz está relacionado con:
- La distribución de valores extremos: si X tiene la distribución de valores extremos estándar para mínimos, entonces la distribución condicional de X (dado X ≥ 0) es un Gompertz estándar.
- La distribución exponencial : La distribución exponencial se compone de límites de secuencias de distribuciones de Gompertz (Marshall & Olkin, 2007). En pocas palabras, se puede combinar una serie de distribuciones exponenciales para hacer un Gompertz. Si X tiene una dist. Gompertz básica. (con parámetro de forma a), entonces Y = e X − 1 tiene una distribución exponencial con parámetro de tasa a.
- La Gompertz es una distribución logarítmica-Weibull Esto se debe a que el logaritmo de la tasa de riesgo es lineal en t, dando: λ(t) = exp{α + Βt). El logaritmo de la tasa de riesgo en el Weibull también es lineal en t (Rodríguez).
Otras formas
Existen varias formas de Gompertz, en parte debido a su larga historia. Fue desarrollado por primera vez por Benjamin Gompertz en 1825, como una forma de modelar las tasas de mortalidad específicas por edad. Aunque se usó ampliamente en la época victoriana, la «ley» de Gompertz perdió popularidad a principios del siglo XX, pero recientemente está recuperando terreno en varias formas diferentes, que incluyen:
- El Gompertz generalizado con tres parámetros, introducido por El-Gohary et al. (2013).
- El beta-Gompertz , introducido por Ali et al. (2014), es una versión generalizada con cuatro parámetros.
- La distribución negativa de Gompertz tiene un parámetro de tasa de envejecimiento negativo adicional.
- La distribución generalizada de Gompertz (GGD) difiere de la distribución «regular» en que «tiene una tasa de falla de curva de bañera creciente, constante o decreciente según el parámetro de forma» (El-Gohary et. al).
- La Distribución de Weibull-Gompertz Generalizada Exponenciada generaliza varias distribuciones, incluida la de Gompertz.
Referencias :
El-Gohary, A et. Alabama. (2013). La distribución generalizada de Gompertz. Modelado Matemático Aplicado. Volumen 37, números 1 y 2, enero de 2013, páginas 13 a 24
Johnson, NL, Kotz, S. y Balakrishnan, N. (1994), Distribuciones univariadas continuas (Vol. I, 2.ª ed.), Nueva York: Wiley .
Marshall & Olkin (2007. Distribuciones de vida: estructura de familias no paramétricas, semiparamétricas y paramétricas. Springer Science & Business Media.
Rodríguez, G. Modelos de supervivencia paramétricos. Disponible aquí .
