Contenido de este artículo
Actualizado el 15 de marzo de 2022, por Luis Benites.
Error estándar de la pendiente de regresión: descripción general
Los errores estándar para la regresión son medidas de qué tan dispersas están sus variables y alrededor de la media, μ. El error estándar de la pendiente de regresión, s (también llamado error estándar de estimación) representa la distancia promedio que sus valores observados se desvían de la regresión línea. Cuanto menor sea el valor de «s», más cerca estarán sus valores de la línea de regresión.
Mire el video para obtener una descripción general de los errores estándar en la regresión lineal , incluido el EE para los coeficientes y la pendiente. El video también muestra cómo calcular el error estándar para la pendiente/coeficiente en Excel:
Errores estándar en regresión lineal Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
El error estándar de la pendiente de regresión es un término que probablemente encontrará en AP Statistics . De hecho, encontrará la fórmula en la lista de fórmulas de estadísticas AP que se le entregó el día del examen.
Error estándar de la fórmula de pendiente de regresión / Instrucciones TI-83
SE de pendiente de regresión = s b 1 = sqrt [ Σ(y i – ŷ i ) 2 / (n – 2) ] / sqrt [ Σ(x i – x ) 2 ].
La ecuación se ve un poco fea, pero el secreto es que no necesitará trabajar la fórmula a mano en la prueba . ¡Incluso si cree que sabe cómo usar la fórmula, le llevará tanto tiempo trabajar que perderá entre 20 y 30 minutos en una pregunta si intenta hacer los cálculos a mano! La calculadora TI-83 está permitida en la prueba y puede ayudarlo a encontrar el error estándar de la pendiente de regresión.
Nota: La TI83 no encuentra directamente el SE de la pendiente de regresión; la «s» informada en la salida es el SE de los residuos, no el SE de la pendiente de regresión. Sin embargo, puede usar la salida para encontrarla con una simple división.
Paso 1: Ingrese sus datos en las listas L1 y L2. Si no sabe cómo ingresar datos en una lista, consulte: Diagrama de dispersión TI-83. )
Paso 2: Presione STAT , desplácese hacia la derecha hasta PRUEBAS y luego seleccione E:LinRegTTest
Paso 3: escriba el nombre de sus listas en Xlist e Ylist . Por ejemplo, escriba L1 y L2 si ingresó sus datos en la lista L1 y en la lista L2 en el Paso 1.
Paso 4: Seleccione el signo de su hipótesis alternativa . Por ejemplo, seleccione (≠ 0) y luego presione ENTER .
Paso 5: Resalte Calcular y luego presione ENTER .
Paso 6: encuentre el valor «t» y el valor «b». Es posible que deba desplazarse hacia abajo con las teclas de flecha para ver el resultado. Por ejemplo, supongamos que su valor t fue -2.51 y su valor b fue -.067.
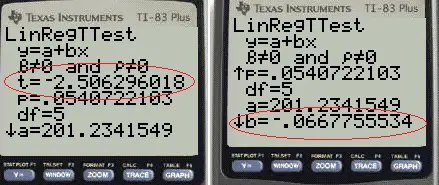
Paso 7: Divide b entre t. Para este ejemplo, -0,67 / -2,51 = 0,027.
El error estándar de la pendiente de regresión para este ejemplo es 0,027.
¡Eso es todo!
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
