Contenido de este artículo
Actualizado el 13 de diciembre de 2021, por Luis Benites.
¿Qué es la estimación de la densidad del kernel?
La estimación de la densidad del núcleo extrapola los datos a una función de densidad de probabilidad de población estimada . Se llama estimación de la densidad del kernel porque cada punto de datos se reemplaza con un kernel, una función de ponderación para estimar el pdf. La función distribuye la influencia de cualquier punto alrededor de una región estrecha que rodea el punto.
La función de densidad de probabilidad resultante es una suma de cada kernel. En muchos sentidos, es como el histograma familiar ; rastrear el contorno de un histograma le brinda una estimación aproximada porque el área debajo de un histograma representa el 100% de la distribución (Pruim, 2011). La principal diferencia entre los histogramas y las densidades de kernel es que en los histogramas, se indica el número de divisiones (o «contenedores»); Por otro lado, establece un ancho para las densidades del núcleo (Stata).
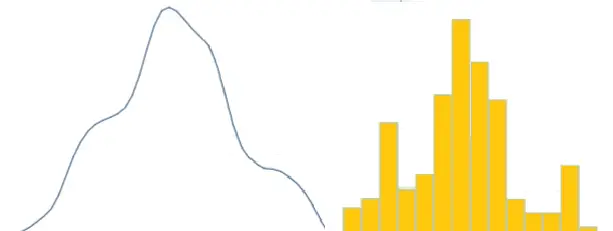
Usos de la estimación de la densidad del kernel
Muchas veces se piensa que las estimaciones kernel son una opción más inteligente que las distribuciones de probabilidad acumulada para mostrar múltiples picos (multimodalidad) (Hart et al.).
Los núcleos también son muy útiles si se trata de estimaciones de densidad específicas. En algunos casos, las densidades pueden ser casi imposibles de calcular sin núcleos. Por ejemplo, algunos tipos de datos circulares se pueden modelar mejor con un kernel de densidad de von Mises, que tiene dos propiedades importantes: el kernel es simétrico y disminuye cuanto más se aleja del punto central del kernel (Pewsky et al. 2013). Otros tipos comunes incluyen:
| Tipo de núcleo | Apoyo | Fórmula |
| Coseno | |μ| ≤1 | 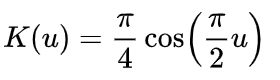 |
| gaussiano | Todos | 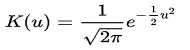 |
| Epanechnikov (parabólica) | μ ≤ 1 | 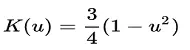 |
| Cuártico (bipeso) | μ ≤ 1 | 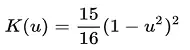 |
| Triángulo | μ ≤ 1 | 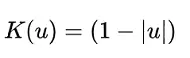 |
| tricubo | μ ≤ 1 | 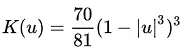 |
| Tripeso | μ ≤ 1 | 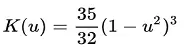 |
| Uniforme | μ ≤ 1 | 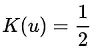 |
Referencias
Esquivar, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Hart, J. et al. Kernel Testing como alternativa al análisis de χ 2
para investigar la distribución de rasgos cuantitativos. 2009. Recuperado el 15 de junio de 2020 de: http://www.stat.tamu.edu/~hart/compare.pdf
Pruim, R. Fundamentos y aplicaciones de estadística: una introducción usando R. American Mathematical Society. 2011.
Stata. Kdensidad .
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
