Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 1 de febrero de 2022, por Luis Benites.
¿Qué es la Máxima Verosimilitud?
La máxima verosimilitud es una forma de encontrar la función más probable para explicar un conjunto de datos observados.
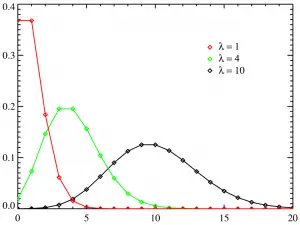
La familia de distribuciones de Poisson.
En estadística elemental, generalmente se le da un modelo para encontrar probabilidades. Por ejemplo, se le puede pedir que encuentre la probabilidad de que X sea mayor que 2, dada la siguiente distribución de Poisson :
X ~ Poisson (2.4)
En este ejemplo, se le da el parámetro , λ, de 2.4 para la distribución de Possion. En la vida real, no puede darse el lujo de que le den un modelo: tendrá que ajustar sus datos a un modelo. Ahí es donde entra en juego la Máxima Verosimilitud (MLE).
MLE toma distribuciones de probabilidad conocidas (como la distribución normal ) y compara conjuntos de datos con esas distribuciones para encontrar una coincidencia adecuada para los datos. Una Familia de distribuciones puede tener una cantidad infinita de parámetros posibles. Por ejemplo, la media de la distribución normal podría ser igual a cero, o podría ser igual a diez mil millones y más. La estimación de máxima verosimilitud es una forma de encontrar los parámetros de la población que es más probable que hayan generado la muestra que se está probando. El grado de coincidencia de los datos con el modelo se conoce como » bondad de ajuste «.
Por ejemplo, un investigador podría estar interesado en averiguar el aumento de peso promedio de las ratas que comen una dieta particular. El investigador no puede pesar todas las ratas de la población, por lo que toma una muestra. Las ganancias de peso de las ratas tienden a seguir una distribución normal; La estimación de máxima verosimilitud se puede utilizar para encontrar la media y la varianza del aumento de peso en la población general en función de esta muestra.
MLE elige los parámetros del modelo en función de los valores que maximizan la función de probabilidad.
La función de probabilidad
La probabilidad de una muestra es la probabilidad de obtener esa muestra, dado un modelo de distribución de probabilidad especificado. La función de verosimilitud es una forma de expresar esa probabilidad: los parámetros que maximizan la probabilidad de obtener esa muestra son los estimadores de máxima verosimilitud.
Supongamos que tiene un conjunto de variables aleatorias X 1 , X 2 …X n tomadas de una distribución de población desconocida con parámetro Θ. Esta distribución tiene una función de densidad de probabilidad (PDF) de f(X i ,Θ) donde f es el modelo, X i es el conjunto de variables aleatorias y Θ es el parámetro desconocido. Para la función de máxima verosimilitud, desea saber cuál es el valor más probable de Θ, dado el conjunto de variables aleatorias X i . La función de densidad de probabilidad conjunta para este ejemplo es:
![]()
En realidad, encontrar la función de máxima verosimilitud implica cálculo. Más específicamente, maximizar el PDF. Si no está familiarizado con la maximización de funciones, es posible que le guste esta calculadora Wolfram .
Siguiente : Algoritmo EM .
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
