Expectativa condicional: definición y ejemplo paso a paso

Actualizado el 3 de febrero de 2022, por Luis Benites.

Es posible que desee leer este otro artículo primero: ¿Qué es la probabilidad condicional?

La expectativa condicional (también llamada media condicional o valor esperado condicional ) es simplemente la media , calculada después de que ha ocurrido un conjunto de condiciones previas. Dicho de manera más formal, la expectativa condicional, E[X|Y], de una variable aleatoria es el valor esperado de esa variable, calculado con respecto a su distribución de probabilidad condicional. También puedes decir que E[X|Y] es la función de Y que es la mejor aproximación para X (o, igualmente, la función de X que es la mejor aproximación para Y).

Fórmula y ejemplo resuelto

Supongamos que tenemos dos variables aleatorias discretas X e Y. con x ∈ Range(X), la condición esperada de Y dado X = x: Nota: X dado Y = y se define de la misma manera (simplemente cambie las variables).

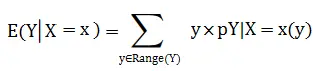
La fórmula puede parecer un poco desalentadora, pero en realidad es bastante simple de usar. Lo que le dice que haga es encontrar las proporciones de la parte «condicional» (todos los valores donde X = 1), multiplicarlos por los valores de Y, luego sumarlos todos (Σ es notación de suma ). El proceso se vuelve mucho más simple si crea una tabla de distribución conjunta .

Pregunta de ejemplo : ¿Cuál es E(Y |X = 1), la expectativa condicional de Y, dado que X = 1? Solución: Paso 1: Encuentra la suma del valor «dado» (X = 1). Esto ya se da en la columna total de nuestra tabla: 0,03 + 0,15 + 0,15 + 0,16 = 0,49.

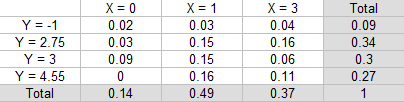
Paso 2: Divida cada valor en la columna X = 1 por el total del Paso 1 :

• 0,03 / 0,49 = 0,061
• 0,15 / 0,49 = 0,306
• 0,15 / 0,49 = 0,306
• 0,16 / 0,49 = 0,327

Paso 3: Multiplique cada respuesta del Paso 2 por el valor Y correspondiente (en la columna de la izquierda):

• 0,0612244898 * -1 = -0,061
• 0,306122449 * 2,75 = 0,842
• 0,306122449 * 3 = 0,918
• 0,3265306122 * 4,55 = 1,486

Paso 3: Sume los valores del Paso 2:
E(Y|X = 1) = -0.061 + 0.842 + 0.918 + 1.486 = 3.19

E(Y|X = 1) = 3,19

Caso continuo

Para distribuciones continuas , las expectativas primero deben definirse mediante un proceso de limitación . El resultado es una función de yyx que puedes interpretar como una variable aleatoria . Básicamente, una integral representa el proceso límite y reemplaza las sumas del ejemplo anterior. La fórmula se convierte en:

Cuando tratamos con variables aleatorias continuas, no tenemos las probabilidades individuales para cada x que teníamos en el ejemplo de variable aleatoria anterior. En cambio, lo que tiene es una función de densidad de probabilidad para cada valor de x individual. Para obtener el valor esperado, integra estos pdf en un pequeño intervalo para forzar esencialmente al pdf a que le dé una probabilidad aproximada. Luego, como en los pasos anteriores, resume todo.