Contenido de este artículo
- 0
- 0
- 0
- 0
Actualizado el 23 de agosto de 2021, por Luis Benites.
¿Qué es el índice de diversidad de Simpson?
El índice de diversidad de Simpson (SDI) mide la diversidad de la comunidad. Aunque se usa comúnmente para medir la biodiversidad, también se puede usar para medir las diferencias de diversidad de las poblaciones en escuelas, comunidades y otros lugares.
El rango es de 0 a 1, donde:
- Las puntuaciones altas (cerca de 1) indican una gran diversidad.
- Las puntuaciones bajas (cercanas a 0) indican baja diversidad.
Uno de los aspectos más útiles del índice es comparar dos conjuntos de datos para ver cuál es más diverso. Por ejemplo, si uno tiene un SDI de 0,5 y otro tiene un SDI de 0,35, entonces el conjunto con el SDI de 0,5 es más diverso.
Mire el video para obtener una descripción general, o lea a continuación:
Índice de diversidad de Simpson 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
Cálculos
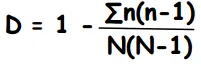Donde:
- n = número de individuos de cada especie
- N = número total de individuos de todas las especies
Los siguientes pasos de solución explican cómo resolver el problema a mano. De hecho, utilicé Open Office Math para resolver este problema. Puede descargar la hoja de trabajo de ODS, con las fórmulas, aquí .
Ejemplo de pregunta: ¿Cuál es el índice de diversidad de Simpson para la siguiente tabla de 5 especies?
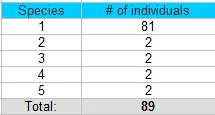
Paso 1: Inserte el número total en el conjunto (89) en la fórmula N (N – 1) y resuelva :
N (N – 1) = 89 (89 -1) = 7832
Deje este número a un lado por un momento.
Paso 2: Calcular n(n – 1).
- Reste 1 de cada cuenta individual (vea la tercera columna en la tabla a continuación).
- Tome cada respuesta de (1) y multiplique por cada n (vea la cuarta columna).
- Sume todos los valores de (2) para obtener 6488.
Paso 3: Calcular D:
- Divida su respuesta del Paso 2 por su respuesta del Paso 1,
- Resta tu respuesta de 1.
D = 1 – (6488 / 7832) = 0,17.
El índice de diversidad para este conjunto en particular es 0,17.
El índice de diversidad de Simpson no puede ser negativo. Si es así, verifique sus cálculos en busca de errores aritméticos.
Referencias
Beyer, WH CRC Standard Mathematical Tables, 31ª ed. Boca Raton, FL: CRC Press, págs. 536 y 571, 2002.
Dodge, Y. (2008). La Enciclopedia Concisa de Estadística . Saltador.
Levine, D. (2014). Incluso usted puede aprender estadísticas y análisis: una guía fácil de entender sobre estadísticas y análisis, 3.ª edición. Pearson FT Press
Wheelan, C. (2014). Estadísticas desnudas . WW Norton y compañía
Redactor del artículo
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
