Contenido de este artículo
Actualizado el 10 de noviembre de 2021, por Luis Benites.
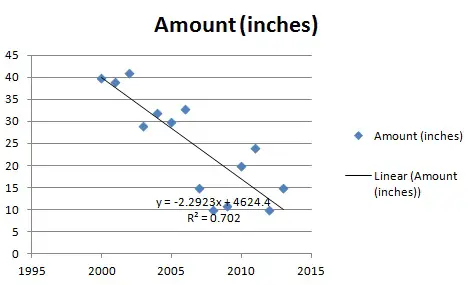
Análisis de regresión.
La regresión a la media tiene que ver con cómo se igualan los datos. Básicamente establece que si una variable es extrema la primera vez que la mide, estará más cerca del promedio la próxima vez que la mida. En términos técnicos, describe cómo una variable aleatoria que está fuera de la norma eventualmente tiende a volver a la norma. Por ejemplo, sus probabilidades de ganar en una máquina tragamonedas siguen siendo las mismas. Es posible que alcance una «racha ganadora», que es, técnicamente hablando, un conjunto de variables aleatorias fuera de la norma. Pero juega a la máquina el tiempo suficiente y las variables aleatorias retrocederán a la media (es decir, «volverán a la normalidad») ¡y terminarás perdiendo!
Ejemplo de la vida real
El maleficio de Sports Illustrated es un excelente ejemplo de regresión a la media. La maldición afirma que quienquiera que aparezca en la portada de SI tendrá un mal año (o años) siguiente. Pero el “gafe” es en realidad una regresión hacia la media. La mayoría de los jugadores tienen buenos juegos y tienen malos juegos. Una racha ganadora suele ser solo eso: una racha de suerte. Y lleva a estar en la portada de SI. Pero es estadísticamente probable que sea seguido por una caída al rendimiento promedio.
¿Por qué ocurre la regresión a la media?
La regresión a la media generalmente ocurre debido a un error de muestreo . Una buena técnica de muestreo es tomar muestras al azar de la población. Si no lo hace (es decir, si toma una muestra asimétrica), entonces sus resultados pueden ser anormalmente altos o bajos para el promedio y, por lo tanto, regresarían a la media. La regresión a la media también puede ocurrir porque toma una muestra muy pequeña y no representativa ( por ejemplo, el 1 por ciento más alto de la población o el diez por ciento más bajo).
Fórmula para el porcentaje de regresión a la media
Puede usar la siguiente fórmula para encontrar el porcentaje para cualquier conjunto de datos:
Porcentaje de regresión a la media = 100(1-r)
donde r es el coeficiente de correlación .
¿Por qué 1-r?
Nota : para comprender esta discusión, debe estar muy familiarizado con r, el coeficiente de correlación.
El porcentaje de regresión a la media tiene en cuenta la correlación entre las variables . Tome dos extremos:
si r=1 (es decir, correlación perfecta), entonces 1-1 = 0 y la regresión a la media es cero. En otras palabras, si sus datos tienen una correlación perfecta, nunca regresarán a la media.
Con una r de cero, hay un 100 por ciento de regresión a la media. En otras palabras, los datos con una r de cero siempre regresarán a la media.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
