Actualizado por ultima vez el 10 de noviembre de 2021, por Luis Benites.
La varianza residual (también llamada varianza no explicada o varianza de error ) es la varianza de cualquier error (residual) .
La definición exacta depende del tipo de análisis que esté realizando . Por ejemplo, en el análisis de regresión , las fluctuaciones aleatorias causan variaciones alrededor de la línea de regresión «verdadera» (Rethemeyer, nd). La varianza total de una línea de regresión se compone de dos partes: varianza explicada y varianza no explicada . La varianza no explicada es simplemente lo que queda cuando se resta la varianza debida a la regresión de la varianza total de la variable dependiente (Neal & Cardon, 2013).
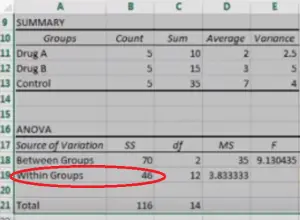
En ANOVA, la varianza dentro de los grupos y la varianza residual se refieren a lo mismo.
En el modelado multinivel , la varianza residual es un reflejo del efecto dentro de los grupos (Garson, 2019). Los coeficientes de varianza residual grandes indican grandes diferencias dentro de los grupos (Xie, 2009). En ANOVA, la variación dentro del grupo es sinónimo de varianza residual.
Símbolo de varianza residual
Los símbolos σ o σ 2 se usan a menudo para denotar una varianza no explicada. Asegúrese de conocer la intención del autor antes de intentar interpretar la varianza residual: σ también puede significar la desviación estándar , la desviación estándar de la muestra o el error estándar de las estimaciones de los coeficientes (Rethemeyer, sin fecha).
Coeficiente de no determinación
La varianza residual, 1 – r 2 a veces se denomina coeficiente de no determinación . El coeficiente de determinación, R 2 , muestra cómo las diferencias en una variable pueden explicarse por una diferencia en una segunda variable. Por lo tanto, el 100% de la varianza de una variable dependiente puede explicarse por r 2 más la “desconocida”: la varianza no explicada (Meyers et al., 2006).
Referencias
Garson, D. (2019). Modelado multinivel: aplicaciones en STATA®, IBM® SPSS®, SAS®, R y HLM™ . 1ra Edición.
Meyers, L. et al. (2006). Investigación Multivariada Aplicada: Diseño e Interpretación .
Neale, M. y Cardón, L. (2003). Metodología para Estudios Genéticos de Gemelos y Familias (Nato Science Series D) . Saltador.
Rethemeyer, K. Términos, símbolos y expresiones de uso común. Recuperado el 27 de abril de 2019 de: https://www.albany.edu/faculty/kretheme/PAD705/SupportMat/CourseTerms.pdf
Xie, Y. (2009). Metodología Sociológica Volumen 39: 1ª Edición . Wiley-Blackwell.
