Actualizado por ultima vez el 31 de diciembre de 2021, por Luis Benites.
Los eventos mutuamente inclusivos tienen cierta superposición entre sí. Por ejemplo, los eventos «comprar un sistema de alarma» y «comprar asientos de cubo» se incluyen mutuamente, ya que ambos eventos pueden ocurrir al mismo tiempo. En otras palabras, el comprador de un automóvil puede optar por comprar una alarma y asientos de cubo. En un diagrama de Venn , esta superposición se muestra como una intersección de dos círculos:
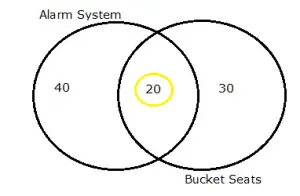
Diagrama de Venn que muestra que 20 de 40 compradores de alarmas compraron asientos de cubo.
Por otro lado, los eventos mutuamente excluyentes no pueden ocurrir al mismo tiempo. Por ejemplo, no puede obtener un automóvil con asientos de cubo y asientos regulares; tienes que elegir una opción u otra.
Una serie de opciones que van de la mano pueden ser mutuamente incluyentes: conducir un automóvil y tener una licencia de conducir; tener electricidad en su casa y pagar la factura de la luz; trabajar como programador y saber usar una computadora. Otra forma de pensarlo es que dos eventos que se incluyen mutuamente no pueden ocurrir de forma independiente. Si tiene dos eventos que son dependientes de alguna manera, son mutuamente inclusivos.
En términos de probabilidad, dos eventos son mutuamente incluyentes si su intersección es mayor que cero:
P(A o B) > 0.
Determinar la probabilidad mutuamente inclusiva.
Para dos eventos cualesquiera A y B:
P(A o B) = P(A) + P(B) – P(A y B).
Ejemplo de pregunta: si elige una carta de una baraja de cartas estándar, ¿cuál es la probabilidad de obtener una reina o un corazón?
Es posible obtener una reina y un corazón al elegir una carta de una baraja de cartas. La reina de corazones es la intersección P(A y B), entonces:
P(Conseguir una reina o Conseguir un corazón) = P(reina) + P(corazón) – P(reina de corazones) =
4/52 + 13/ 52 – 1/52 = 16/52.
Esto se llama la regla de la suma . Se puede utilizar para calcular probabilidades de eventos mutuamente excluyentes y mutuamente inclusivos. En el caso de eventos mutuamente excluyentes, la intersección P(A y B) es cero.
Siguiente : La regla de la suma .
