Actualizado por ultima vez el 20 de marzo de 2022, por Luis Benites.
En combinatoria , los números de Stirling del segundo tipo nos dicen cuántas formas hay de dividir un conjunto de n objetos (todos diferentes, o al menos todos etiquetados) en k subconjuntos no vacíos . Los k subconjuntos no están etiquetados.
Escribimos los números de Stirling del segundo tipo como S(n,k) o:
.
Ejemplos de números de Stirling de segunda clase
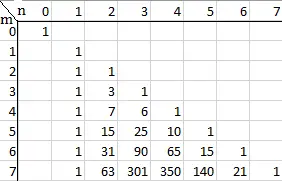
¿Qué es S(3,3)? Esta pregunta pregunta «¿De cuántas maneras podemos dividir un conjunto de tres elementos en tres subconjuntos?» Un conjunto de tres elementos, digamos, el conjunto {0,1,2}, se puede dividir en tres subconjuntos exactamente de una manera: {1,2,3}, por lo que S(3,3) es solo 1. De hecho, dado que un conjunto de k elementos siempre se puede dividir en un conjunto de k subconjuntos no vacíos exactamente de una manera, S(n,n) siempre es 1.
S(3,2) será el número de formas en que podemos dividir nuestro conjunto de tres elementos en dos subconjuntos. Hay tres formas posibles de hacer esto; cada uno divide el conjunto en dos piezas formadas por un elemento y dos elementos. Usando nuestro conjunto de ejemplo de {0,1,2}, podemos llegar a:
{{0,1}{2}}
{{0}{1,2}}
{{1}{0,2}}.
Entonces S(3,2)= 3.
S(3,1) es el número de formas en que podemos dividir nuestros elementos en un solo subconjunto; dado que la única posibilidad de eso es el conjunto que incluye todos los elementos, {0,1,2}, S(3,1) también es 1. Esto también se puede generalizar; S(n,1) = 1 para cada n.
La siguiente tabla (de Quaintance, 2015) muestra las primeras posibilidades para los números de Stirling del segundo tipo:
Cálculo de números de Stirling de segunda clase
Hay dos formas de calcular los números de Stirling del segundo tipo. Primero, se pueden calcular recursivamente; es decir, con referencia a números de Stirling de segundo tipo de orden inferior.
S(m,n) = S(m – 1,n – 1) + nS(m – 1,n).
Donde:
- m es el número de elementos en el conjunto original,
- n es el número de subconjuntos.
Esta sencilla fórmula facilita la elaboración de tablas de números de Stirling del segundo tipo, o la búsqueda de un número cuando conocemos las cifras de conjuntos más pequeños.
Vimos arriba que S(3,2) = 3 y S(3,1) = 1. Podemos usar estos dos hechos para permitirnos encontrar S(4,2), ya que con m = 4 y 2 = n, la fórmula anterior se convierte en:
S(4,2) = S(3,1) + 2 * S(3,2) = 1 + 2 * 3 = 7.
También hay una fórmula que se puede usar para calcular S(n,k) para cualquier n o k. Esto está dado por
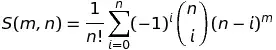Aquí ! significa un factorial , y el Σ grande significa que lo que viene después se suma de i = 0 a n.
Referencias
Cuantificación, J. (2015). Identidades combinatorias para números de Stirling: las notas inéditas de HW Gould . World Scientific, 27 de octubre.
