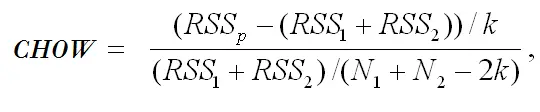Prueba de Chow: definición y ejemplos

Actualizado el 21 de julio de 2024, por Luis Benites.

¿Qué es una prueba de Chow?

La prueba de Chow le dice si los coeficientes de regresión son diferentes para conjuntos de datos divididos. Básicamente, prueba si una línea de regresión o dos líneas de regresión separadas se ajustan mejor a un conjunto dividido de datos.

Conjuntos de datos divididos y la prueba de Chow

A veces, sus datos tendrán un punto de ruptura o un punto estructural (un período de cambio significativo o violento), lo que dividirá un conjunto de datos en dos partes. Por ejemplo:

• Donaciones dadas a una organización antes y después de un desastre natural.
• Cotizaciones bursátiles antes y después del Black Friday.
• Precios de la vivienda antes y después de un cambio de interés significativo.
• Precios de los activos antes y después de la guerra civil.

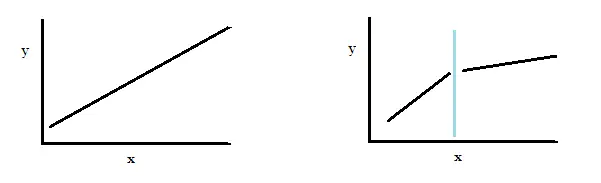
El conjunto de datos de la izquierda tiene una sola línea de regresión. El conjunto de la derecha tiene un punto de quiebre en el medio y dos líneas de regresión.

Si las dos partes se pueden representar mediante una sola línea de regresión, decimos que la regresión se puede “agrupar”.

Digamos que su análisis de regresión lineal de dos partes de un conjunto de datos (que se muestra a la derecha) resultó en las siguientes dos ecuaciones de regresión lineal :

• Primera parte de los datos: y _t = X ₁ *b ₁ + μ ₁
• Segunda parte de los datos: y _t = X ₂ *b ₂ + μ ₂

La prueba de Chow le diría si los coeficientes b ₁ = b ₂ y μ 1 = μ ₂ . Si son iguales, el conjunto de datos se puede representar con una sola línea de regresión.

Ejecución de la prueba

La hipótesis nula de la prueba es que no hay punto de ruptura (es decir, que el conjunto de datos se puede representar con una sola línea de regresión).

1. Ejecute una regresión para todo el conjunto de datos (la «regresión agrupada»). Recopile los datos de Suma de cuadrados del error .
2. Ejecute regresiones separadas en cada mitad del conjunto de datos. Recopile los datos de la Suma de cuadrados del error para las dos regresiones.
3. Calcule la estadística Chow F utilizando el SSE de cada submuestra . La fórmula es: donde:
   • RSS _p = línea de regresión agrupada (combinada).
   • RSS ₁ = línea de regresión antes de la ruptura.
   • RSS ₂ = línea de regresión después de la ruptura.
4. Encuentre el valor F-crítico de la tabla F.
5. Rechace la hipótesis nula si su valor F calculado cae dentro de la región de rechazo (es decir, si el valor F calculado es mayor que el valor F crítico).

Referencia :
Chow, GC (1960), «Pruebas de igualdad entre conjuntos de coeficientes en dos regresiones lineales», Econometrica, 28, 591-605.