Prueba de rango logarítmico, LRT ponderada: LRT estratificada: definiciones, ejemplos

Actualizado el 11 de abril de 2022, por Luis Benites.

1. ¿Qué es la prueba de rango logarítmico?

La prueba de rango logarítmico es una prueba de hipótesis no paramétrica para comparar las distribuciones de supervivencia de dos muestras . A menudo se utiliza en ensayos clínicos para comparar la experiencia de supervivencia de dos grupos de personas. Por ejemplo, es posible que desee probar si el Medicamento A aumenta el tiempo de supervivencia en comparación con el Medicamento B.

Esta prueba le dirá si hay una diferencia, pero no le dará detalles sobre el tamaño de la diferencia ni le dará un intervalo de confianza .

Otras pruebas de diferencias, como la prueba t de dos muestras, no son apropiadas para este tipo de datos, porque los datos suelen estar muy sesgados.

Ejecución de la prueba

La hipótesis nula de la prueba de rango logarítmico es que no hay diferencia en las probabilidades de supervivencia entre los dos grupos. La probabilidad se calcula para algún evento, que podría ser la muerte u otro evento significativo.

La prueba compara las estimaciones de las funciones de riesgo de los dos grupos en cada momento del evento observado. El número observado y esperado de eventos se calcula en uno de los grupos en cada tiempo de evento observado, luego estos resultados se suman para obtener un resumen general de todos los puntos en el tiempo cuando ocurrió un evento. Esta prueba no suele calcularse a mano, debido a la complejidad de los cálculos.

suposiciones

Los supuestos para la prueba de rango logarítmico son:

• La censura (que ocurre cuando no se sabe el tiempo exacto de supervivencia) no debe estar relacionada con el pronóstico,
• Las probabilidades de supervivencia son iguales para los sujetos reclutados en cualquier momento del estudio,
• Los hechos ocurrieron en el tiempo especificado.

variaciones

2. Prueba ponderada de rango logarítmico

La prueba de rango logarítmico ponderado se usa si desea comparar grupos pero quiere dar más importancia («peso») a ciertos eventos.

Si bien la prueba de rango logarítmico nos permite encontrar la distribución de supervivencia relativa para dos muestras, asume que cada punto en el tiempo tiene la misma importancia. Funciona mejor cuando los peligros (amenazas a la supervivencia) son relativamente constantes en el tiempo o proporcionales . La prueba de rango logarítmico ponderado nos permite tener en cuenta que los diferentes momentos son más o menos importantes. Esto lo convierte en una prueba muy útil para cuando los riesgos no son proporcionales; por ejemplo, para cuando las probabilidades de supervivencia son mucho mayores al principio del tiempo y disminuyen al final.

La prueba de rango logarítmico ponderado se usa a menudo en estudios clínicos cuando un determinado momento o momentos son más relevantes que otros. Por ejemplo, en un ensayo clínico que probó un nuevo y agresivo fármaco contra el cáncer, es posible que desee centrarse más en las amenazas de supervivencia a corto plazo (causadas por la toxicidad potencial del fármaco) que en la posibilidad de mejorar a largo plazo.

Un tratamiento conservador, por otro lado, puede tardar un tiempo en marcar una diferencia para los participantes de un estudio. En ese caso, nos gustaría pesar más para más adelante.

Elección de pesos para la prueba de rango logarítmico ponderado

Los pesos deben elegirse en función de la información previa que tenga sobre su tema de investigación, y no en las curvas de supervivencia. Querrá establecer sus pesos cuando diseñe su experimento, no después de mirar su conjunto de datos. Si elige pesos basados ​​en su conjunto de datos o curvas de supervivencia, corre el riesgo de un razonamiento circular en sus resultados.

La fórmula para la prueba ponderada está dada por

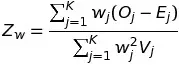
Aquí O _j -E _j es una medida de cómo difieren los peligros por tiempo j. La ponderación viene dada por el w _j ; números no negativos que definen qué tan importante es ese punto en el tiempo para nuestra investigación. Si W _j es constante sobre j, obtenemos la estadística de prueba de rango logarítmico estándar.

Ni la prueba de rango logarítmico ni la prueba de rango logarítmico ponderado se calculan normalmente a mano; la aritmética es demasiado extensa.

3. Prueba de rango logarítmico estratificada

Prueba de rango logarítmico estratificado : se utiliza cuando se desea controlar un factor como la edad, el sexo, el peso o alguna otra variable. Por ejemplo, puede tener dos grupos y controlar el género (hombres, mujeres) dando cuatro grupos o estratos posibles.

La prueba de rango logarítmico nos permite encontrar la distribución de supervivencia relativa para dos muestras, pero en su forma original no nos permite ajustar ningún factor especial que pueda afectar eso. La prueba de clasificación logarítmica estratificada es la prueba que usaría al analizar la distribución de supervivencia de dos muestras que se dividen en dos o más grupos o «estratos» según criterios comunes que afectan el resultado.

Uso de la prueba de clasificación logarítmica estratificada

Suponga que desea encontrar la distribución de supervivencia relativa de dos grupos de personas con viruela; un grupo toma un medicamento nuevo y otro toma un placebo . La prueba de rango logarítmico le daría una estadística que describe esto. Pero sus muestras no son uniformes ; se pueden dividir en segmentos masculinos y femeninos. Ajustar esto en su análisis puede brindarle más información.

El uso de una prueba de clasificación logarítmica estratificada podría volverse importante si los hombres o las mujeres fueran particularmente susceptibles a morir de viruela, y el grupo de placebo y de prueba no incluyera exactamente el mismo número de participantes masculinos y femeninos. Así que el género sería lo que llamamos un factor de confusión . Es una variable que está asociada con cada miembro del conjunto de datos y también está causalmente relacionada con el resultado de interés (supervivencia).

No es necesariamente binario ; por ejemplo, en un estudio sobre pacientes con diabetes, uno podría querer estratificar según el peso. El peso está causalmente relacionado con la supervivencia, y puede dividir sus muestras en tantos grupos discretos como sea conveniente para su estudio.

Prerrequisitos y supuestos de la prueba de clasificación logarítmica estratificada

Antes de usar la prueba de clasificación logarítmica estratificada, querrá verificar que su variable de interés no sea una variable de confusión. Solo es un factor de confusión si está realmente en la vía causal desde la exposición (es decir, la variable independiente ) hasta el resultado (es decir, la variable dependiente ).

El uso de la prueba de rango logarítmico estratificado también supone que el efecto (supervivencia) es similar en ambos estratos del factor de confusión.

Ejecución de la prueba de clasificación logarítmica estratificada

Para ejecutar la prueba de clasificación logarítmica estratificada:

• Calcule la estadística de prueba de rango logarítmico sobre cada estrato individual.
• Tome la media ponderada de esas estadísticas de prueba de rango logarítmico individuales.

Sean U _s  el estadístico de prueba de rango logarítmico estratificado y U _i sean los estadísticos de prueba de rango logarítmico individuales sobre el conjunto de j estratos. Entonces puedes escribir esto como:

Referencias:

Universidad Stanford. Prueba de rango logarítmico. Recuperado el 3 de septiembre de 2017 de: https://web.stanford.edu/~lutian/coursepdf/unitweek3.pdf
Pruebas mejoradas de tipo de rango logarítmico para datos de supervivencia usando pesos adaptables
Prueba de rango logarítmico. Recuperado el 3 de septiembre de 2017 de: http://myweb.uiowa.edu/pbreheny/7210/f15/notes/9-17.pdf
Extensiones de la prueba de rango logarítmico
Prueba de rango logarítmico en neurociencia. Recuperado el 4 de septiembre de 2017 de: http://www.sciencedirect.com/topics/neuroscience/logrank-test
Prueba de rango de registro. Recuperado el 4 de septiembre de 2017 de: https://web.stanford.edu/~lutian/coursepdf/unitweek3.pdf

Artículos relacionados

Prueba de Tarone-Ware