Contenido de este artículo
Actualizado el 11 de noviembre de 2021, por Luis Benites.
¿Qué es la prueba Q de Dixon?
La prueba Q de Dixon, o simplemente la «prueba Q», es una forma de encontrar valores atípicos en conjuntos de datos muy pequeños, normalmente distribuidos . Los conjuntos de datos pequeños generalmente se definen como entre 3 y 7 elementos. Se usa comúnmente en química, donde los conjuntos de datos a veces incluyen una observación sospechosa que es mucho más baja o más alta que los otros valores. Mantener un valor atípico en los datos afecta a cálculos como la media y la desviación estándar , por lo que se deben eliminar los valores atípicos verdaderos.
Dixon ideó muchas ecuaciones diferentes para encontrar verdaderos valores atípicos. La más utilizada se llama R 10 o simplemente la versión «Q», que se usa para probar si un solo valor es un valor atípico en un tamaño de muestra de entre 3 y 7. Dean y Dixon sugirieron varias otras fórmulas en un papel posterior , pero estos no se usan comúnmente. Para obtener una lista completa de fórmulas alternativas para diferentes tamaños de muestra (hasta aproximadamente 30), vaya a: Prueba de Dixon, Fórmulas y tablas alternativas .
Cómo ejecutar la prueba Q de Dixon (R 10 ).
Nota : asegúrese de que su conjunto de datos esté distribuido normalmente antes de ejecutar la prueba; por ejemplo, ejecute una prueba de Shapiro-Wilk . Ejecutarlo en diferentes distribuciones conducirá a resultados erróneos. Un valor extremo puede descartar cualquier prueba de normalidad, así que intente ejecutar esa prueba sin el elemento de datos sospechoso. Si su conjunto de datos aún no cumple con el supuesto de normalidad después de realizar una prueba, entonces no debe ejecutar la prueba Q de Dixon.
Precaución : la prueba no debe usarse más de una vez para el mismo conjunto de datos.
Ejemplo: : ¿Es 167 un valor atípico en este conjunto de datos? Realice la prueba con un nivel de confianza del 95 % (es decir, con un nivel alfa del 5 %).
167, 180, 188, 177, 181, 185, 189
Paso 1: ordene sus datos en orden ascendente (de menor a mayor).
167, 177, 180, 181, 185, 188, 189.
Paso 2: Encuentre la estadística Q usando la siguiente fórmula: Donde:
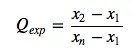
- x 1 es el valor más pequeño (sospechoso),
- x 2 es el segundo valor más pequeño,
- yxn es el valor más grande .
Insertando los valores en la fórmula , obtenemos:
Q = (177 – 167) / 189 – 167 = 10/22 = 0,455.
Paso 3: encuentre el valor crítico Q en la tabla Q (desplácese hasta la parte inferior del artículo para ver la tabla). Para un tamaño de muestra de 7 y un nivel alfa de 5%, el valor crítico es 0,568.
Paso 4: Compare la estadística Q del Paso 2 con el valor crítico Q del Paso 3. Si la estadística Q es mayor que el valor crítico Q, el punto es un valor atípico. Estadístico
Q = 0,455. Q valor crítico = 0,568.
Solución : 0,455 no es mayor que 0,568, por lo que este punto no es un valor atípico en un nivel alfa del 5 %.
Tabla Q de Dixon
Esta tabla muestra los niveles alfa más comunes .10, .05 y .01. Puede encontrar niveles alfa menos comunes en el sitio web de UC Davis .
| Tamaño de la muestra: | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| α = .10: | 0.941 | 0.765 | 0.642 | 0.560 | 0.507 | 0.468 | 0.437 | 0.412 |
| α = .05: | 0.970 | 0.829 | 0.710 | 0.625 | 0.568 | 0.526 | 0.493 | 0.466 |
| α = .01: | 0.994 | 0.926 | 0.821 | 0.740 | 0.680 | 0.634 | 0.598 | 0.568 |
Prueba de Dixon, fórmulas alternativas y tablas .
Encontrar la estadística Q para diferentes tamaños de muestra (n) de entre 8 y 30 (en el Paso 2 anterior):
8< n >10: use R 11 : 11< n >13: use R 21 . 14<n>30: utilice R22 .
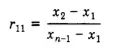
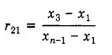
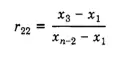
| norte | α = 0,001 | α = 0,002 | α = 0,005 | α = 0,01 | α = 0,02 | α = 0,05 | α = 0,1 | α = 0,2 |
| 8 | 0.799 | 0.769 | 0.724 | 0.682 | 0.633 | 0.554 | 0.480 | 0.386 |
| 9 | 0.750 | 0.720 | 0.675 | 0.634 | 0.586 | 0.512 | 0.441 | 0.352 |
| 10 | 0.713 | 0.683 | 0.637 | 0.597 | 0.551 | 0.477 | 0.409 | 0.325 |
| norte | α = 0,001 | α = 0,002 | α = 0,005 | α = 0,01 | α = 0,02 | α = 0,05 | α = 0,1 | α = 0,2 |
| 11 | 0.770 | 0.746 | 0.708 | 0.674 | 0.636 | 0.575 | 0.518 | 0.445 |
| 12 | 0.739 | 0.714 | 0.676 | 0.643 | 0.605 | 0.546 | 0.489 | 0.420 |
| 13 | 0.713 | 0.687 | 0.649 | 0.617 | 0.580 | 0.522 | 0.467 | 0.399 |
| norte | α = 0,001 | α = 0,002 | α = 0,005 | α = 0,01 | α = 0,02 | α = 0,05 | α = 0,1 | α = 0,2 |
| 14 | 0.732 | 0.708 | 0.672 | 0.640 | 0.603 | 0.546 | 0.491 | 0.422 |
| 15 | 0.708 | 0.685 | 0.648 | 0.617 | 0.582 | 0.524 | 0.470 | 0.403 |
| dieciséis | 0.691 | 0.667 | 0.630 | 0.598 | 0.562 | 0.505 | 0.453 | 0.386 |
| 17 | 0.671 | 0.647 | 0.611 | 0.580 | 0.545 | 0.489 | 0.437 | 0.373 |
| 18 | 0.652 | 0.628 | 0.594 | 0.564 | 0.529 | 0.475 | 0.424 | 0.361 |
| 19 | 0.640 | 0.617 | 0.581 | 0.551 | 0.517 | 0.462 | 0.412 | 0.349 |
| 20 | 0.627 | 0.604 | 0.568 | 0.538 | 0.503 | 0.450 | 0.401 | 0.339 |
| 25 | 0.574 | 0.550 | 0.517 | 0.489 | 0.457 | 0.406 | 0.359 | 0.302 |
| 30 | 0.539 | 0.517 | 0.484 | 0.456 | 0.425 | 0.376 | 0.332 | 0.278 |
Referencia :
RB Dean y WJ Dixon (1951) Estadísticas simplificadas para números pequeños de observaciones. Anal. Chem., 1951, 23 (4), 636–638. Encontrado en línea aquí .
Rorabacher, David B. (1991) Tratamiento estadístico para el rechazo de valores desviados: valores críticos del parámetro ‘Q’ de Dixon y relaciones de subrango relacionadas con un nivel de confianza del 95 %. Química Analítica 63, núm. 2 (1991): 139–46. Encontrado en línea aquí .
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
