Contenido de este artículo
Actualizado el 8 de noviembre de 2021, por Luis Benites.
La corrección de Yates se hace para tener en cuenta el hecho de que tanto la prueba de chi-cuadrado de Pearson como la prueba de McNemar están sesgadas hacia arriba para una tabla de contingencia de 2 x 2 . Un sesgo hacia arriba tiende a hacer que los resultados sean más grandes de lo que deberían ser. Si está creando una tabla de contingencia de 2 x 2 que utiliza cualquiera de estas dos pruebas, generalmente se recomienda la corrección de Yates, especialmente si las frecuencias de celda esperadas están por debajo de 10 (algunos autores ponen esa cifra en 5).
Mire el video para ver un ejemplo.
Ejemplo de corrección de Yates Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
¿Por qué se utiliza la corrección de Yates?
Las pruebas de chi 2 están sesgadas hacia arriba cuando se usan en tablas de contingencia de 2 x 2. La razón es que la distribución estadística Chi 2 es continua y la tabla de contingencia 2 x 2 es dicotómica (es decir, no es continua, hay dos variables). Las matemáticas que prueban esto están más allá del alcance de este sitio (estaríamos profundizando en algunas pruebas serias aquí). Todo lo que realmente necesita saber es que si sus frecuencias de celda esperadas están por debajo de 10, probablemente debería usar la corrección de Yates.
Cálculo de la corrección de Yates
¿ Necesita ayuda con una pregunta de tarea? ¡Mira nuestra página de tutoría!
Para aplicar la corrección de Yates, reste .5 de la diferencia numérica entre las frecuencias observadas y las frecuencias esperadas . La fórmula parece complicada, pero es solo la fórmula de Chi 2 con la resta de .5:
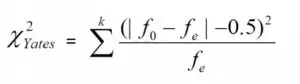
La fórmula de corrección de Yates.
Debe hacer esto para las cuatro celdas de su cálculo.
Ejemplo : su tabla de contingencia le brinda valores de frecuencia de celda observados y esperados de:
Celda 1: 220, 210.22
Celda 2: 7, 9.12
Celda 3: 2, .22
Celda 4: 21, 17.12
La corrección de Yates sería:
Celda 1: ( |220 – 210.22|-.5) 2 /210.22
Celda 2: (|7 – 9.12|-.5) 2 /9.12
Celda 3: (|2 – .22|-.5) 2 /.22
Celda 4: ( |21 – 17,12|-,5) 2 / 17,12
= 0,41 + 0,29 + 7,44 + 0,67
= 8,81
Argumentos de por qué no se debe usar la Corrección de Yates
Aunque algunas personas recomiendan que use la corrección solo si su frecuencia celular esperada es inferior a 10 o incluso 5, otras recomiendan que no la use en absoluto . Un gran cuerpo de investigación ha encontrado que la corrección es demasiado estricta. Varios investigadores, incluido Yates, han utilizado datos estadísticos conocidos para probar si la corrección funciona. Si está utilizando un programa estadístico como R para calcular el valor crítico de chi-cuadrado para una tabla de contingencia, el programa generalmente lo obligará a incorporar la corrección. Sin embargo, saber que la corrección puede ser demasiado estricta le permite juzgar sus datos.
Referencias
Greenwood, P. (1996). Una guía para las pruebas de chi-cuadrado (serie de Wiley en probabilidad y estadística) 1.ª edición. Wiley Interscience.
Yates, F. (1934). Tablas de contingencia. Revista de la Sociedad Real de Estadística, 1, 217-235.
Si elige no utilizar la corrección, puede citar uno de los siguientes artículos, que argumentan que la Corrección de Yates es demasiado estricta:
Camilli, G. & Hopkins, KD (1979). Pruebas de asociación en tablas de contingencia 2 * 2 con tamaños de muestra muy pequeños. Boletín Psicológico, 86, 1011-1014. Artículo en línea .
Larntz, K. (1978). Comparaciones de muestras pequeñas de niveles exactos para las estadísticas de bondad de ajuste de chi-cuadrado. Revista de la Asociación Estadounidense de Estadística, 73, 253-263. Artículo en línea.
Thompson, B. (1988). Mal uso de las estadísticas de prueba de tabla de contingencia de chi-cuadrado. Investigación educativa y psicológica, 8(1), 39-49. Artículo en línea.
Este artículo ofrece un resumen de los argumentos:
Hitchcock, David B. (2009). Yates y tablas de contingencia: 75 años después. Recuperado el 08/04/2015 de: Universidad de Carolina del Sur.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo:
