Actualizado por ultima vez el 3 de noviembre de 2021, por Luis Benites.
¿Qué es una relación estadística?
Las relaciones en probabilidad y estadística generalmente pueden ser una de tres cosas: determinista, aleatoria o estadística. Una relación estadística es una mezcla de relaciones deterministas y aleatorias.
- Una relación determinista implica una relación exacta entre dos variables. Por ejemplo, supongamos que gana $10 por hora. Por cada hora que trabajas, ganas diez dólares más.
- Una relación aleatoria es un nombre un poco inapropiado, porque no hay relación entre las variables. Sin embargo, los procesos aleatorios pueden hacer que parezca que existe una relación. Por ejemplo, gasta $20 en boletos de lotería y gana $25. Esa “ganancia” se debe al azar, pero podría hacerle pensar que por cada $20 que gaste en boletos, ganará $25 más (lo cual, por supuesto, es falso).
- Una relación estadística es una mezcla de las dos relaciones anteriores. Es una relación que es en parte determinista y en parte aleatoria. Por ejemplo, existe una relación estadística entre la ingesta de calorías y el aumento de peso. Pero la relación no es exacta: cuánto peso ganas depende de muchos otros factores y algún elemento de aleatoriedad. ¿Esa barra de chocolate de 200 calorías realmente contiene 200 calorías? ¿De verdad te comiste exactamente una porción de helado?
Cómo saber si existe una relación estadística
Existe una relación estadística si un cambio en una variable (X) resulta en un aumento sistemático en otra (Y). El aumento sistemático no tiene que ser exacto (es decir, diez unidades cada vez), pero debe ser aproximadamente el mismo («alrededor de diez»). Las formas de medir las relaciones estadísticas incluyen:
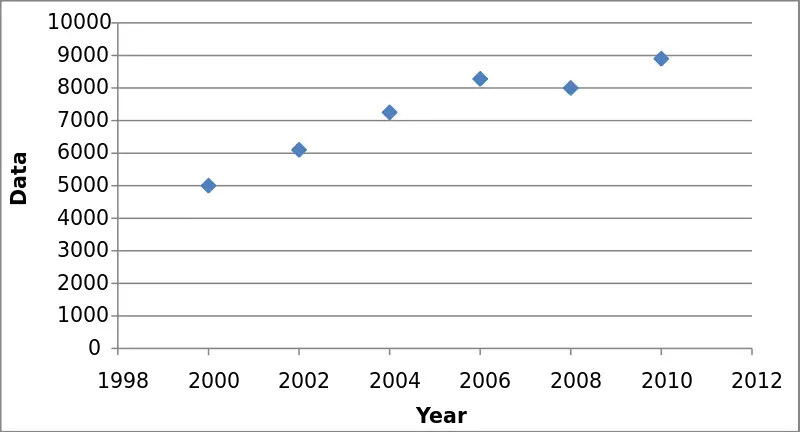
Un gráfico de dispersión.
- Un gráfico de líneas o un diagrama de dispersión pueden darle una idea acerca de las relaciones. Esto no tiene que ser una línea recta (una » relación lineal «), pero debe mostrar un patrón definido (una curva parabólica es un ejemplo de una «relación no lineal»). El patrón no tiene que ser perfecto (como en el gráfico de dispersión anterior) y, a veces, se denomina » tendencia «.
- La correlación es una medida de la fuerza de la relación. La R de Pearson es una medida numérica de la fuerza de la correlación. Un valor de 0 significa que no hay relación y 1 significa una relación perfecta.
- La D de Cohen también es una medida de la fuerza de la relación. En general, los valores cercanos a cero son relaciones “pequeñas” y los valores cercanos a uno son relaciones “grandes”.
Siguiente : Causalidad vs. Correlación
Referencias
Gonick, L. y Smith, W. (1993). The Cartoon Guide to Statistics Paperback – Ilustrado. Harper Perennial.
