Actualizado por ultima vez el 29 de enero de 2022, por Luis Benites.
¿Qué es la varianza relativa?
La varianza relativa (RV) es una medida de error, o cuánto puede variar el «ruido» de un punto de datos o conjunto de puntos de datos. RV no tiene una definición universal y no se usa muy a menudo en estadísticas, excepto en términos muy informales. Las diferentes definiciones incluyen (sin ningún orden en particular):
Definición 1
La varianza relativa es la varianza , dividida por el valor absoluto de la media (s 2 /|x̄|). También puede multiplicar el resultado por 100 para obtener el porcentaje de RV. Nota : los dos términos varianza relativa y porcentaje de varianza relativa a veces se usan indistintamente.
Definición 2
Este tiene más sentido para mí personalmente, aunque estoy seguro de que otras opiniones difieren. Hermance (2013) define la RV en términos de lluvia. La varianza de la precipitación en una determinada estación se compone de tres varianzas diferentes. El RV se utiliza para «… definir el efecto que tiene la variabilidad de las precipitaciones de un mes determinado sobre la variabilidad de las precipitaciones durante toda la estación para la estación». Es una definición relativamente simple, con esta fórmula (donde sd = desviación estándar):
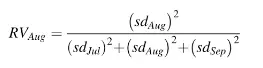
Varianza relativa de las lluvias de agosto, basada en tres meses (julio, agosto, septiembre).
Definición 3
Encontré una sola referencia a otra fórmula (muy similar), en una publicación del Departamento de Comercio de EE. UU., que definía RV como «la varianza dividida por el cuadrado de la estimación». La última parte podría ser una lección sobre cuántas definiciones pueden volverse confusas. Dice que la “…raíz cuadrada del RV se define como el coeficiente de variación ”.

- Según esta definición, el cuadrado del coeficiente de variación debe ser igual al RV al cuadrado.
- El coeficiente de variación se define como la desviación estándar dividida por la media.
- Por lo tanto, la varianza dividida por el cuadrado de la estimación, al cuadrado, debe ser igual a la desviación estándar dividida por la media
.
Esto no equivale, así que tenga cuidado cuando utilice el RV como cálculo.
También he visto RV calculado como:
- La raíz cuadrada de la varianza dividida por la media:
- La desviación estándar dividida por la media .
- Una constante multiplicada por un diámetro, dividida por un peso ( aquí ).
En resumen, no existe una fórmula estándar, así que tenga mucho cuidado si usa esta estadística; puede terminar confundiendo a sus lectores.
Referencias :
Hermance, J. (2013). Variabilidad histórica de las precipitaciones en el Sahel oriental africano de Sudán: implicaciones para el desarrollo . Springer Science & Business Media.
Poole, C. et. Alabama. (2001). Cromatografía relativa de capa fina, un estudio práctico. pág. 318 .
Var relativo Manual de referencia de la gráfica de datos . 3 de septiembre de 1996.
Departamento de Comercio de los Estados Unidos. (1968). Agrostan: un estudio de caso para el censo agrícola mundial de 1970, volumen 3
willhelm-Welmer, F. (2012). Evaluaciones Estadísticas en Exploración de Yacimientos Minerales. Springer Science & Business Media.

