Corrección de Bessel: ¿Por qué usar N-1 para la varianza/desviación estándar?

Actualizado el 19 de marzo de 2022, por Luis Benites.

¿Qué es la corrección de Bessel?

La corrección de Bessels se refiere al “n-1” que se encuentra en varias fórmulas, incluidas las fórmulas de varianza muestral y desviación estándar muestral . Esta corrección se hace para corregir el hecho de que estas estadísticas muestrales tienden a subestimar los parámetros reales encontrados en la población.

Bessel también se encuentra en los cálculos de la prueba T de Student .

Cálculos de corrección de varianza y desviación estándar de Bessel

Por lo general, usará la siguiente fórmula para encontrar la varianza de la muestra: La fórmula para la desviación estándar de la muestra es similar: como puede ver, ambas fórmulas tienen n-1 en el denominador, donde n es el tamaño de la muestra .

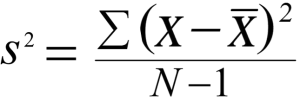
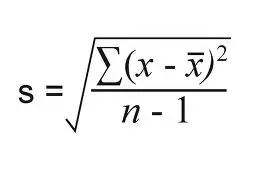
Entonces, ¿por qué restamos 1 cuando usamos estas fórmulas?

La respuesta simple: los cálculos tanto para la desviación estándar de la muestra como para la varianza de la muestra contienen un pequeño sesgo (esa es la forma estadística de decir «error»). La corrección de Bessel (es decir, restar 1 del tamaño de la muestra) corrige este sesgo. En otras palabras, normalmente obtendrá una respuesta más precisa si usa n-1 en lugar de n .

La respuesta más técnica:
cuando tiene una población completa y calcula cualquier parámetro (como la varianza de la población o la desviación estándar de la población), sus resultados serán precisos. Eso es porque tienes todos los datos sobre tu población. Sin embargo, cuando trabaja con una muestra , solo tiene una pequeña fracción de la población para trabajar. Por lo tanto, sus respuestas no van a ser tan precisas como las que habría obtenido si tuviera todo el conjunto de datos para trabajar.

En el caso de la varianza de la muestra y la desviación estándar, la estadística particular con la que está trabajando es la media de la muestra (x̄) en lugar de la media de la población (μ). Cualquier valor de x en su muestra estará más cerca de x̄ que de μ.

Este hecho altera las sumas de cuadrados (en el numerador de las fórmulas anteriores). La suma de cuadrados de μ va a ser mayor que la suma de cuadrados de x̄. En otras palabras, los cálculos de muestra con n en el denominador casi siempre serán más altos que los cálculos con n-1 en el denominador (Warne, 2017). Cuando resta 1 del tamaño de la muestra, resulta que está haciendo un ajuste bastante bueno para la suma deflactada de la figura de los cuadrados siempre que n no sea enorme (Edelman, 2018).

¿Cuándo debo usar la corrección de Bessel?

Para tamaños de muestra pequeños, la corrección de Bessel será bastante severa. Si tiene una muestra pequeña, es muy poco probable que sea una muy buena estimación de la media de la población de todos modos. Si tiene un tamaño de muestra muy grande, se acercará a un punto en el que las estadísticas de su muestra serán casi iguales a los parámetros de su población. En ese caso, la corrección de Bessel simplemente no es necesaria en absoluto.

Warne (2017) recomienda usar la corrección de Bessel solo si tiene una muestra lo suficientemente grande y si realmente está tratando de aproximarse a la media de la población. Si solo está interesado en encontrar la media de la muestra y no desea extrapolar sus hallazgos a la población, simplemente omita la corrección.

Referencias

Edelman, A. (2018). Recuperado el 25 de julio de 2017 de: http://web.mit.edu/18.06/www/Spring17/Statistics-and-PCA.pdf
LaValle, S. (2016). Prueba de la hipótesis .
Warne, T. (2017). Estadísticas para las ciencias sociales: un enfoque de modelo lineal general . Prensa de la Universidad de Cambridge.