Actualizado por ultima vez el 28 de abril de 2022, por Luis Benites.
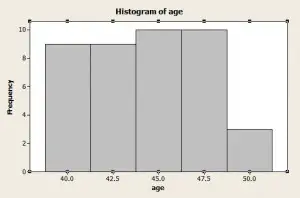
Datos agrupados que se muestran en un histograma.
La corrección de Sheppard para errores de agrupación son ajustes a momentos de muestra calculados para datos agrupados (es decir, datos que se han agrupado ). La corrección lleva el nombre de WF Shepard, quien señaló que cuando se calculan momentos para distribuciones de frecuencia continuas, se supone que los datos se centran alrededor de los puntos medios del intervalo de clase . Esta suposición errónea introduce «errores de agrupación» en el cálculo de momentos. Los errores de agrupación solo ocurren en momentos pares (por ejemplo, segundo y cuarto momentos), por lo que la corrección no es necesaria para momentos impares.
¿Qué tipo de datos se pueden corregir?
La corrección de Sheppard tiene algunas restricciones severas, que la hacen aplicable solo a un pequeño rango de distribuciones. La corrección sólo debe hacerse a datos con las siguientes características:
- Las frecuencias deberían reducirse a cero tanto en la dirección positiva como en la negativa. En otras palabras, las frecuencias deben ser simétricas y disminuir gradualmente (como el comportamiento que vería en una distribución normal ).
- Las variables deben ser continuas . El método no es adecuado para variables discretas .
- Los intervalos de clase deben tener el mismo ancho.
- Los intervalos de clase deben ser más de 1/20 del rango total .
Además, el Libro de texto de muestreo y atributos de Sharma señala que el ajuste no debe hacerse para:
- Distribuciones en forma de J.
- Distribuciones altamente sesgadas .
- Distribuciones en forma de U.
- Muestras de menos de 1000 artículos (con muestras más pequeñas, el error de muestreo será un problema mayor que los errores de agrupación).
Fórmulas de corrección de Sheppard
- Primer momento ( media ): no se necesita corrección.
- Segundo momento (varianza): estimación calculada de la varianza (m 2 – (i 2 /12) donde i es el ancho del intervalo de clase.
- Tercer momento ( sesgo ): no se necesita corrección.
- Cuarto momento ( curtosis ): estimación calculada para la curtosis (m 4 ) – ½i 2 m 2 + (7/240)i 4
Ejemplo
La distribución anterior tiene los siguientes momentos alrededor de la media:
- metro 1 = 0
- m2 = 2,64
- m3 = 0,08
- m 4 = 28,30
Usa la corrección de Sheppard para estos momentos. Tenga en cuenta que el intervalo de clase para la distribución es 2.
Solución:
- m 1 = 0 ; no se necesita corrección.
- metro 2 = metro 2 – (yo 2 /12) = 2,64 – 2 2 /12 = 0,33 = 2,3 .
- m3 = 0,08 ; _ no se necesita corrección
- m 4 = (m 4 ) – ½i 2 m 2 + (7/240)i 4 = 28,30 – 5,28 + 0,12 = 23,14 .
Referencias:
AK Sharma. Libro de texto de Muestreo y Atributos.
