Criterio de información de Akaike: definición, fórmulas

Actualizado el 12 de septiembre de 2021, por Luis Benites.

¿Qué es el criterio de información de Akaike?

El criterio de información de Akaike (AIC) compara la calidad de un conjunto de modelos estadísticos entre sí. Por ejemplo, podría estar interesado en qué variables contribuyen al bajo nivel socioeconómico y cómo las variables contribuyen a ese estado. Supongamos que crea varios modelos de regresión para varios factores como la educación, el tamaño de la familia o el estado de discapacidad; El AIC tomará cada modelo y los clasificará de mejor a peor. El “mejor” modelo será el que no quede ni demasiado ni demasiado ajustado.

Aunque el AIC elegirá el mejor modelo de un conjunto, no dirá nada sobre la calidad absoluta . En otras palabras, si todos sus modelos son malos, elegirá lo mejor de un grupo malo. Por lo tanto, una vez que haya seleccionado el mejor modelo, considere ejecutar una prueba de hipótesis para averiguar la relación entre las variables de su modelo y el resultado de interés.

Cálculos

El criterio de información de Akaike generalmente se calcula con software. La fórmula básica se define como:
AIC = -2(log-verosimilitud) + 2K
Donde:

• K es el número de parámetros del modelo (el número de variables en el modelo más el intercepto).
• Log-verosimilitud es una medida del ajuste del modelo. Cuanto mayor sea el número, mejor será el ajuste. Esto generalmente se obtiene de la producción estadística.

Para tamaños de muestra pequeños (n/K < ≈ 40), utilice el AIC de segundo orden:
AIC _c = -2(log-verosimilitud) + 2K + (2K(K+1)/(nK-1))
Donde:

• n = tamaño de la muestra,
• K= número de parámetros del modelo,
• Log-verosimilitud es una medida del ajuste del modelo.

Una fórmula alternativa para el tipo de análisis de regresión de mínimos cuadrados para errores normalmente distribuidos : Donde:

• = Suma Residual de Cuadrados /n,
• n = tamaño de la muestra ,
• K es el número de parámetros del modelo.

Tenga en cuenta que con esta fórmula, la varianza estimada debe incluirse en el recuento de parámetros.

Puntajes Delta y Pesos Akaike

Las puntuaciones de AIC se informan como puntuaciones de ΔAIC o pesos de Akaike. Los puntajes ΔAIC son los más fáciles de calcular e interpretar.

El ΔAIC es la diferencia relativa entre el mejor modelo (que tiene un ΔAIC de cero) y cada uno de los demás modelos del conjunto. La fórmula es:
ΔAIC = AIC _i – min AIC.
Donde:

• AIC _i es la puntuación para el modelo particular i.
• min AIC es la puntuación del «mejor» modelo.

Burnham y Anderson (2003) dan la siguiente regla general para interpretar las puntuaciones ΔAIC:

• ΔAIC < 2 → evidencia sustancial para el modelo.
• 3 > ΔAIC 7 → menos soporte para el modelo.
• ΔAIC > 10 → el modelo es improbable.

Los pesos de Akaike son un poco más engorrosos de calcular pero tienen la ventaja de que son más fáciles de interpretar: dan la probabilidad de que el modelo sea el mejor del conjunto. La fórmula es:

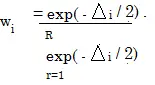
Referencias

:
Burnham y Anderson (2003) Selección de modelos e inferencia de modelos múltiples: un enfoque teórico práctico de la información. Springer Science & Business Media.