Actualizado por ultima vez el 14 de marzo de 2022, por Luis Benites.
La distribución Beta Prime es una distribución de probabilidad continua definida en el intervalo [0, ∞). La distribución tiene colas gruesas que decrecen polinomialmente. En las estadísticas bayesianas , la distribución es una familia conjugada de distribuciones previas en el parámetro de probabilidades de la distribución binomial .
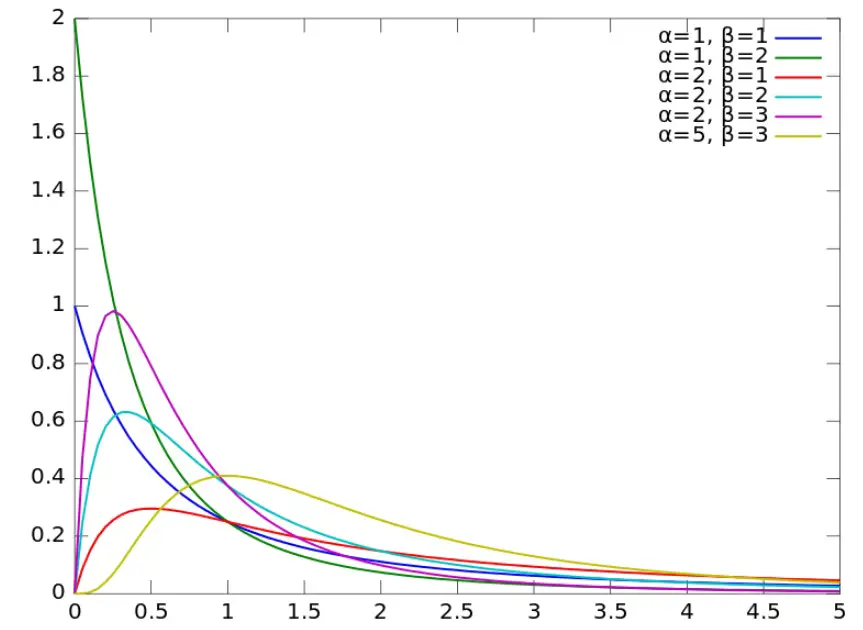
PDF de beta-prime.
La distribución tiene muchos otros nombres, incluidos: beta tipo II, gamma compuesta, relación gamma, beta inversa (o invertida), Pearson tipo VI y relación de varianza. La relación entre la distribución beta y la beta prima es la siguiente: si una variable aleatoria Z es de una distribución beta, X = Z -1 – 1 es de una distribución beta prima [2].
La función de densidad de probabilidad estandarizada para la distribución primaria beta son los parámetros de forma y Β(α, β) es la función beta . Algunas definiciones incluyen un parámetro de escala, λ, pero esto no es común; La mayoría de las definiciones se definen para λ = 1 [2].
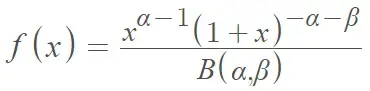
La función de distribución acumulativa es: F(x) = I x/(1+x) (α, β).
La media es α(β – 1) para β > 1.
La moda es (α – 1)/ (α + β – 2) para α > 1, β > 1.
La mediana no puede expresarse en una expresión de forma cerrada simple .
Casos Especiales de la Distribución Beta Prime Generalizada
La distribución beta prima tiene muchos casos especiales, superpuestos con algunas familias de distribuciones de probabilidad. Por ejemplo, la distribución de la función potencia es un caso especial de la distribución beta prima cuando Β es negativo. Otros casos especiales notables incluyen [3]:
- distribución de rebabas ,
- distribución de dagum ,
- Logística de distribución ,
- Distribución Lomax ,
- Distribución F.
Referencias
[1] Fishman, G. (2001). Simulación de eventos discretos: modelado, programación y análisis. Saltador.[2] Laurent, S. (2019). R-Bloggers: la distribución beta del tercer tipo. Recuperado el 31 de diciembre de 2021 de: https://www.r-bloggers.com/2019/07/the-beta-distribution-of-the-third-kind-or-generalised-beta-prime/
[3] Crooks, G. Encuesta de distribuciones de probabilidad simples, continuas y univariadas . Recuperado el 31 de diciembre de 2021 de: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.372.3694&rep=rep1&type=pdf

