Actualizado por ultima vez el 29 de septiembre de 2021, por Luis Benites.
¿Qué es una Distribución Beta?
Una distribución Beta es una forma versátil de representar resultados para porcentajes o proporciones. Por ejemplo, ¿cuál es la probabilidad de que un candidato deshonesto gane las próximas elecciones presidenciales? Se podría pensar que la probabilidad es 0,2. Tu amigo podría pensar que es 0,15. La distribución beta te da una manera de describir esto.
Una razón por la que esta función es confusa es que hay tres «Betas» con las que lidiar, y todas tienen significados diferentes:
- Beta(α, β): el nombre de la distribución de probabilidad.
- B(α, β ): el nombre de una función en el denominador del pdf . Esto actúa como una » constante de normalización » para asegurar que el área bajo la curva del pdf sea igual a 1.
- β: el nombre del segundo parámetro de forma en el pdf.
La distribución beta básica también se denomina distribución beta de primer tipo . La distribución beta del segundo tipo es otro nombre para la distribución beta principal .
Función de densidad de probabilidad
La fórmula general para la función de densidad de probabilidad es: donde: α y β son dos parámetros de forma positivos que controlan la forma de la distribución.
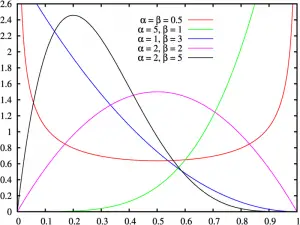
La Distribución Beta pdf.
Opciones de software
La mayoría de los paquetes de software tienen opciones para la distribución beta.
Mathematica
Implemente una distribución beta escribiendo BetaDistribution[alpha,beta].
R
dbeta(x, forma1, forma2, ncp = 0, log = FALSO)
pbeta(q, forma1, forma2, ncp = 0, cola inferior = VERDADERO, log.p = FALSO)
qbeta(p, forma1, forma2, ncp = 0, cola inferior = VERDADERO, log.p = FALSO)
rbeta(n, forma1, forma2, ncp = 0)
donde:
- x, q = vector de cuantiles .
p = vector de probabilidades. - n = # de observaciones.
- forma1, forma2 = parámetros de forma α y β
- ncp = parámetro de no centralidad.
- registro, registro.p = lógico; si es VERDADERO, las probabilidades p se dan como log(p).
- cola.inferior = lógico; si es VERDADERO (predeterminado), las probabilidades son P[X ≤ x], de lo contrario, P[X > x].
Distribución Beta de Excel: BETA.DIST & INV.BETA
Mire el video para ver un ejemplo de BETA.DIST:
Distribución Beta de Excel (BETA.DIST) 
Mira este video en YouTube .
¿No puedes ver el vídeo? Haga clic aquí
El formato de distribución beta de Microsoft Excel depende de la versión de Excel que esté utilizando; Excel 2010 y posteriores usan la función BETA.DIST, mientras que las versiones anteriores usan BETADIST. Necesitará saber alfa y beta, los cuales se refieren a los parámetros que describen la distribución. Se necesitan cinco entradas:
- El valor en el que desea evaluar la función .
- Alfa y Beta, los parámetros de la distribución que determinan la forma.
- El límite inferior y superior.
Se necesita una entrada adicional para la distribución beta de Excel 2010: acumulativa. Acumulativo es un valor lógico que determina la forma de la función y puede ser VERDADERO (devuelve la función de distribución acumulativa) o FALSO (devuelve la función de densidad de probabilidad).
Problema de ejemplo: Calcule una función de distribución acumulativa para una distribución beta en Excel en 0,5 con un alfa de 9, una beta de 10, un límite inferior de 0 y un límite superior de 1.
Excel 2007 y anteriores:
Paso 1: escriba el valor donde desea evaluar la función en la celda A1. Para este ejemplo, escriba «.5» en la celda A1.
Paso 2: escriba el valor de alfa en la celda A2 y luego escriba el valor de beta en la celda A1. Para este ejemplo, escriba «9» en la celda A2 y luego escriba «10» en la celda A3.
Paso 3: Escriba el límite inferior en la celda A4 y luego escriba el límite superior en la celda A5. Para este ejemplo, escriba «0» en la celda A4 y luego escriba «1» en la celda A5.
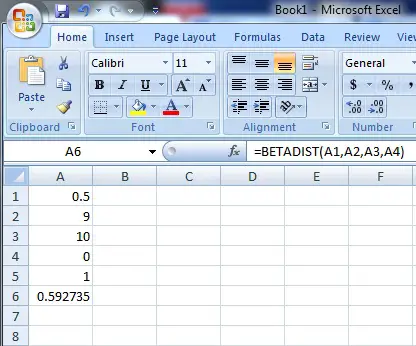
Paso 4: escriba la función de distribución beta en la celda A6. El formato de la función es =BETADIST(valor,alfa,beta,límite inferior,límite superior). Para este ejemplo, escriba «=BETADIST(A1,A2,A3,A4,A5)» en la celda A6. Presiona “Enter” para ver el resultado de la distribución beta, que es 0.592735.
Excel 2010 y posterior
Paso 1: siga los pasos 1 a 3 en la sección anterior de Excel 2003-2007.
Paso 2: escriba la función de distribución beta en la celda A6. El formato de la función es =BETA.DIST(valor,alfa,beta,acumulativo,límite inferior,límite superior). Para este ejemplo, escriba «=BETA.DIST(A1,A2,A3,TRUE,A4,A5)» en la celda A6. Presiona “Enter” para ver el resultado de la distribución beta, que es 0.592735.
Función de densidad beta
La distribución Beta es una excelente manera de representar resultados como probabilidades o proporciones. Los valores de α y Β determinan la forma de la función de densidad beta . Por ejemplo, si α < 1 y Β < 1, la forma del gráfico será una “U” (vea el diagrama rojo en la imagen de arriba, y si α = 1 y Β = 2, el gráfico es una línea recta; si mira el gráfico de arriba, la línea azul es casi una línea recta: eso es porque α = 1 y Β = 3.
La función de probabilidad P(x) y la función de distribución D(x) para la Distribución Beta son:
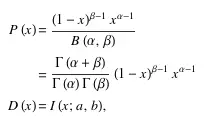
Aplicaciones de la Función de Densidad Beta
La distribución beta se utiliza para muchas aplicaciones, incluidas las pruebas de hipótesis bayesianas , la regla de sucesión (un ejemplo famoso es el tratamiento del problema del amanecer de Pierre-Simon Laplace) y el modelado de duración de tareas. La distribución beta es especialmente adecuada para sistemas de control de proyectos/planificación como PERT y CPM porque la función está restringida por un intervalo con un valor mínimo (0) y máximo (1).
Referencias :
Abramowitz, M. y Stegun, IA (Eds.). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas , novena edición. Nueva York: Dover, págs. 944-945, 1972
Evans, M.; Hastings, N.; y Peacock, B. «Distribución Beta». cap. 5 en Distribuciones estadísticas, 3ª ed . Nueva York: Wiley, págs. 34-42, 2000.
