Distribución de Dirichlet: definición simple, PDF, media

Actualizado el 20 de abril de 2022, por Luis Benites.

1. ¿Qué es una distribución de Dirichlet?

Una distribución de Dirichlet (pronunciada Deer-eesh-lay ) es una forma de modelar funciones de masa de probabilidad aleatoria (PMF) para conjuntos finitos . También se utiliza a veces como a priori en las estadísticas bayesianas . La distribución crea n números positivos (un conjunto de vectores aleatorios X ₁ …X _n ) que suman 1; Por lo tanto, está estrechamente relacionado con la distribución multinomial , que también requiere n números que suman 1.

La distribución lleva el nombre del matemático belga del siglo XIX Johann Dirichlet .

2. ¿Qué son los PMF aleatorios?

Cuando se introduce la probabilidad en las estadísticas básicas, uno de los temas comunes que surgen es lanzar un dado justo. El “dado justo” es casi con seguridad un mito; Los procesos de fabricación son bastante buenos, pero no son perfectos. Si lanza 1000 dados, las probabilidades teóricas de que aparezca cualquier número en particular (es decir, 1, 2, 3, 4, 5 o 6) son 1/6. Sin embargo, no obtendrá esa distribución exacta en un experimento real debido a defectos de fabricación. Ningún dado tiene el peso perfecto: siempre habrá un poco de balanceo hacia un lado u otro del dado. Si tiene diez dados, cada dado tendrá su propia función de masa de probabilidad (PMF).

Otro ejemplo de un PMF aleatorio es la distribución de palabras en libros y otros documentos; Un libro de k palabras de longitud se puede modelar mediante una distribución de Dirichlet con un PMF de longitud k .

3. El proceso de Dirichlet

El proceso de Dirichlet es una forma de modelar la aleatoriedad de una función de masa de probabilidad (PMF) con opciones ilimitadas (por ejemplo, una cantidad ilimitada de dados en una bolsa). El proceso es similar al de la urna de Polya , solo que en lugar de tener un número fijo de colores de bolas, tienes una cantidad ilimitada .

• Comience con una urna vacía.
• Elige al azar una bola de color y colócala en la urna.
• Luego elige una opción:
  1. Elige al azar una bola de color y colócala en la urna.
  2. Retire al azar una bola de color de la urna, luego vuelva a colocarla con otra bola del mismo color.

A medida que aumenta el número de bolas en la urna, disminuye la probabilidad de elegir un nuevo color . La proporción de bolas en la urna después de una cantidad infinita de sorteos es un proceso de Dirichlet. Para ver un ejemplo de un proceso de Dirichlet, consulte: Proceso de restaurante chino .

4. PDF/Media/Varianza

La explicación anterior da un esquema de una distribución de Dirichlet. La matemática real detrás de la distribución es un poco más compleja. Para comprender completamente la distribución, debe tener una idea sobre:

• Distribuciones Beta .
• Cambio de Variables .
• Funciones gamma .
• Distribuciones multivariadas.

PDF

La función de densidad de probabilidad (PDF) es: Donde: y a ₁ , …, am son parámetros con a _i > 0 para i=1,…,m.

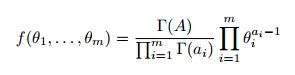
Significar

La media de θ _j es:
E(θ _j ) = a _j / A.

Diferencia

La varianza de θ _j es:
var(θ _j ) = a _j / A (A + 1) – a _j / A (A + 1).

5. Similitud con otras distribuciones

• El Dirichlet es la generalización multivariante de la distribución beta . Es una extensión de la distribución beta para modelar probabilidades de dos o más eventos disjuntos ; cuando m=2 (ver PDF a continuación), la distribución de Dirichlet es igual a la PDF de la distribución beta.
• El Dirichlet iguala la distribución uniforme cuando todos los parámetros (α ₁ …α _k ) son iguales.
• La distribución de Dirichlet es un conjugado anterior a la distribución categórica y las distribuciones multinomiales. Una variante compuesta es el multinomio de Dirichlet.

Referencias :

Blackwell, D. y MacQueen, JB (1973). Distribuciones de Ferguson a través de esquemas de urnas de Polya. Ana. estatista _ 2, 1, 353-355.
Cifarelli, DM y Regazzini, E. (1990). Funciones de distribución de medios de un Dir. proceso. Ana. Estadístico. 18 429-442
Emilion, R. (2005). Proceso de distribuciones aleatorias. Afrika Stat, vol 1, 1, pp. 27-46, http://www.ufrsat.org/jas (contenido).
Everitt, BS; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press.
Ferguson, TS (1974). Distribuciones previas sobre espacios de medidas de probabilidad. Ana. Estadístico. 2 615-629.
Kotz, S.; et al., editores. (2006), Enciclopedia de Ciencias Estadísticas , Wiley.
Kingman, JFC (1975). Distribuciones aleatorias discretas. J.Roy. Estadístico. Soc. B, 37, 1-22.