Distribución de valor extremo y la teoría del valor extremo

Actualizado el 15 de noviembre de 2021, por Luis Benites.

Distribuciones de probabilidad > Distribución de valor extremo y teoría del valor extremo

¿Qué es una distribución de valor extremo?

Una distribución de valor extremo es un modelo límite para los máximos y mínimos de un conjunto de datos. Modela qué tan grandes (o pequeños) serán probablemente sus datos. Por ejemplo, supongamos que desea construir un dique para protegerse contra las marejadas ciclónicas. Puede usar datos históricos de tormentas para crear una distribución límite que le indique qué tan grandes es probable que crezcan las olas y cuándo es probable que se rompa el dique. Puede ser útil pensar en el límite como un punto de falla, un punto que, si se excede, ocurrirá algún tipo de falla o evento de fin de vida.

La idea básica es que tres tipos de distribuciones de valores extremos ( EVD Tipos I, II y II ) pueden modelar los extremos de cualquier conjunto de datos, siempre que la distribución tenga un «buen comportamiento» (Gumbel, 1958), con la siguientes caracteristicas:

• Es una distribución de probabilidad continua . Una distribución continua tiene un rango de valores que son infinitos y, por lo tanto, incontables . Por ejemplo, el tiempo es infinito: puedes contar desde 0 segundos hasta mil millones de segundos… un billón de segundos… y así sucesivamente, para siempre.
• Tiene inversa . Una distribución inversa es la distribución del recíproco de una variable aleatoria .
• Está formado por variables aleatorias independientes distribuidas de forma idéntica (IID) . Idénticamente distribuido significa que no hay tendencias generales: la distribución no fluctúa y todos los elementos de la muestra se toman de la misma distribución de probabilidad. Es básicamente lo mismo que una muestra aleatoria .

Volver arriba

Tipos de distribución de valores extremos I, II y III

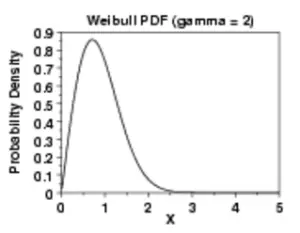
La distribución de Weibull es una forma de modelar valores extremos.

Si genera cualquier cantidad de conjuntos de datos, toma los mínimos y máximos de esos conjuntos y genera una nueva distribución, seguirá uno de los tres tipos de modelos: sin límites superior o inferior (EVD I), limitado en el extremo inferior (EVD II ), o delimitada en el extremo superior (EVD Tipo III) (Haan, 1977).

• EVD Tipo I: Distribución Gumbel (también llamado Tipo Gumbel). Este es el EVD más común y tiene dos formas: una para el mínimo y otra para el máximo, aunque es ilimitada (no restringida a un rango) y se define sobre todo el rango de números reales . La función de densidad de probabilidad tiene solo una forma inmutable que cambia según el parámetro de ubicación, μ. A medida que aumenta μ, la distribución se desplaza hacia la izquierda; A medida que μ disminuye, se desplaza hacia la derecha. Digamos que tiene una lista de niveles mínimos de contaminación para la última década. Podría usar el EVD Tipo I para modelar los niveles mínimos de contaminación para el próximo año. (Más info: ¿Qué es la Distribución Gumbel ?)
• EVD Tipo II: Distribución Fréchet . Esta distribución se utiliza para modelar valores máximos en un conjunto de datos . El Fréchet converge lentamente a 1 y tiene tres parámetros: parámetro de forma, α, parámetro de escala, β y parámetro de ubicación μ. Se define en el intervalo μ ∞; En otras palabras, está acotado (restringido) en el lado inferior. Con el Fréchet se puede modelar una amplia gama de fenómenos como el análisis de inundaciones, las carreras de caballos, la esperanza de vida humana, las precipitaciones máximas y las descargas fluviales en hidrología. (Más información: ¿Qué es la Distribución Fréchet ?)
• EVD Tipo III: Distribución Weibull . La distribución de Weibull se utiliza para evaluar la confiabilidad del producto para modelar los tiempos de falla y el análisis de datos de vida útil. El Weibull es en realidad una familia de distribuciones que puede adoptar muchas formas, según los parámetros que elija. Incluye dos distribuciones exponenciales , una distribución sesgada a la derecha y una distribución simétrica . (Más info: ¿Qué es la Distribución Weibull ?)

Volver arriba

La distribución generalizada de valores extremos

La distribución de valores extremos generalizados (GEV) es una distribución de tres parámetros que une las distribuciones de valores extremos de tipo I (Gumbel), tipo II (Fréchet) y tipo III (Weibull). Cuál de los tres modelos que elija depende del comportamiento en la cola de la distribución principal. Sin embargo, por lo general no se conoce el comportamiento de la cola de la población de padres (Holmes, 2015). Si no sabe nada sobre el comportamiento de la cola, entonces es imposible elegir qué modelo podría ser el «mejor». El GEV resuelve este problema combinando las tres distribuciones en una sola forma general.

El CDF para el GEV es: Los parámetros son:

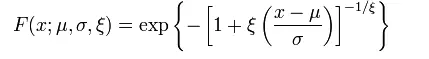
• Parámetro de ubicación , μ,
• Parámetro de escala , σ,
• Parámetro de forma , ξ.

σ y 1 + ξ(x-μ)/σ debe ser mayor que cero. ξ y μ pueden tomar cualquier valor real.
El parámetro de forma define qué distribución adopta la distribución generalizada de valores extremos:

• Cuando el parámetro de forma ξ es igual a 0, el GEV es igual al EVD Tipo I.
• Cuando es mayor que 0, el GEV es igual a EVD Tipo II.
• Cuando ξ es menor que 0, el GEV es igual a EVD Tipo III.

La distribución GEV a veces se denomina distribución Fisher-Tippett , en honor a Ronald Fisher y LHC Tippett. Sin embargo, esto puede causar un poco de confusión porque el caso especial de la distribución de Gumbel también se denomina a veces distribución de Fisher-Tippet. Para evitar confusiones, es mejor referirse a la distribución que abarca los tres tipos (EVD I, II y III) como la distribución de valores extremos generalizada .

¿Cuál es la distribución de valor extremo más grande?

La distribución de valor extremo más grande es otro nombre para la distribución de Gumbel .

La distribución de valor extremo más grande está estrechamente relacionada con la distribución de valor extremo más pequeño: si una variable aleatoria X tiene una distribución de valor extremo más grande, entonces la variable aleatoria −X tiene una distribución de valor extremo más pequeño y viceversa.

Volver arriba

¿Qué es un “Valor extremo”?

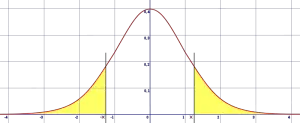
Los valores extremos se encuentran en las colas de una distribución de probabilidad (resaltados en amarillo en la imagen).

Un valor extremo es un valor muy pequeño o muy grande en una distribución de probabilidad . Estos valores extremos se encuentran en las colas de una distribución de probabilidad (es decir, los extremos de la distribución).

El término «valor extremo» puede significar algo ligeramente diferente dependiendo de dónde lo lea. Algunos autores usan el término «valor extremo» como otro nombre para el valor mínimo y/o el valor máximo de una función (es decir, el número más pequeño y/o más grande del conjunto), y otros lo usan como sinónimo de valor atípico . En cálculo , los puntos donde se encuentran los valores máximos y mínimos se denominan extremos , por lo que algunos autores también se refieren a estos puntos como «valores extremos». Sin embargo, en la mayoría de los casos, cuando las personas hablan de valores extremos, generalmente se refieren a valores asociados con la teoría del valor extremo.

Volver arriba

¿Qué es la teoría del valor extremo?

La teoría del valor extremo (EVT) es una rama de la estadística que se ocupa del comportamiento estocástico de los eventos extremos que se encuentran en las colas de las distribuciones de probabilidad. Un modelo estocástico representa una situación donde la incertidumbre está presente. En otras palabras, es un modelo para un proceso que tiene algún tipo de aleatoriedad. EVT tiene como objetivo predecir probabilidades de eventos raros mayores (o menores) que los eventos registrados anteriormente. Por ejemplo, EVT podría usarse en sismología para predecir el próximo megaterremoto en California, el último de los cuales fue en 1857 .

EVT se originó a partir de la astronomía y la necesidad de mantener o rechazar valores atípicos en los datos (Kotz & Nadarajah, 2003). Los valores atípicos son rezagados (valores extremadamente altos o extremadamente bajos) en un conjunto de datos que puede alterar sus estadísticas. Por ejemplo, si estuviera midiendo la longitud de la nariz de los niños, su valor promedio podría perderse si Pinocho estuviera en la clase. EVT se ha convertido en una teoría que es aplicable a casi todas las áreas de la ciencia y los negocios. Por ejemplo, la teoría puede modelar y predecir una amplia gama de fenómenos, como las alturas máximas de las olas del mar o la fortaleza de los mercados financieros (Coles, 2013). La teoría, que utiliza distribuciones de valores extremos, se usa ampliamente en economía, finanzas, ciencia de materiales, ingeniería de confiabilidad y muchos otros campos.

Comparación con CLT

La teoría del valor extremo es muy similar al Teorema del Límite Central (CLT) . Ambas teorías involucran comportamientos limitantes de distribuciones de variables aleatorias independientes e idénticamente distribuidas como n→ ∞, pero hay una clara diferencia: la CLT se refiere al comportamiento de distribuciones enteras de variables aleatorias, mientras que la teoría de valores extremos solo se refiere al comportamiento de las colas de esas distribuciones.

Para poner la diferencia entre EVT y CLT con un poco más de precisión, la CLT describe el comportamiento límite de X ₁ , X ₂ ,…X _n mientras que la teoría del valor extremo describe el comportamiento límite de los extremos max(X ₂ ,…,X _n ) o min(X ₂ ,…,X _n ) (de Haan & Ferreira, 2007).

Volver arriba

Artículos relacionados:

• El problema de los tanques alemanes encuentra máximos de población, dados máximos de muestra.

Referencias

Caltech / Centro de datos de terremotos del sur de California (2013). Terremoto de Fort Tejon
Obtenido el 16 de octubre de 2017 de: http://scedc.caltech.edu/significant/forttejon1857.html.
Coles, S. (2013). Una introducción al modelado estadístico de valores extremos. Springer Science & Business Media.
De Haan, L. y Ferreira, A. (2013). Teoría del valor extremo: una introducción. Springer Ciencia y Negocios.
Fisher, RA, Tippett, LHC (1928). “ Formas limitantes de la distribución de frecuencias del miembro más grande y más pequeño de una muestra. ”Proc. Sociedad Filosófica de Cambridge 24: 180-190.
Gumbel, E. (1958). Estadísticas de Extremos. Nueva York, Prensa de la Universidad de Columbia.
Han, (1977). Métodos Estadísticos en Hidrología. USGS.
Holmes, J. (2015). Carga de viento de estructuras, tercera edición. Prensa CRC.
Kotz y Nadarajah, (2000). Distribución de valor extremo: teoría y aplicaciones. Científico Mundial.
Weibull, W. (1951). “Una función de distribución estadística de amplia aplicabilidad” J. Appl. Mec.-Trans. ASME 18(3), 293-297.