Actualizado por ultima vez el 3 de junio de 2022, por Luis Benites.
¿Qué es la Distribución Tukey Lambda?
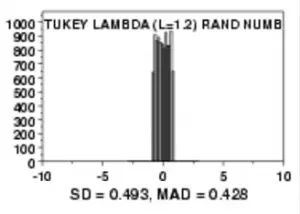
La distribución Tukey Lambda (a veces llamada distribución lambda simétrica ) tiene colas truncadas.
La distribución Tukey Lambda es una familia de distribuciones simétricas con colas truncadas (cortadas).
La distribución se define numéricamente con tres parámetros:
- λ, el parámetro de forma ,
- μ, el parámetro de ubicación ,
- σ, el parámetro de escala .
A diferencia de la mayoría de las otras distribuciones de probabilidad, no existe una fórmula de «talla única» para la función de densidad de probabilidad (PDF) y la función de distribución acumulativa (CDF) . Por lo general, lo verá definido en términos de cuantiles o la siguiente función de distribución: La siguiente imagen muestra dos formas muy diferentes para valores de λ de 0,5 y 5,0:
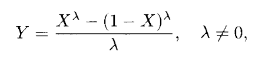
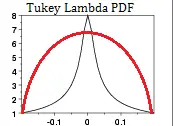
Tukey-Lambda PDF con λ=0.5 (negro) y 5.0 (rojo).
Entonces, aunque no hay un PDF general para todos los valores posibles de λ, se puede generar fácilmente un PDF para valores específicos una vez que conoce la función percentil.
GLD y la función percentil
La distribución lambda generalizada generalmente se define en términos de su función percentil de cuatro parámetros:
![]() . Donde :
. Donde :
0 ≤ y ≤ 1
y
Usos
No es sorprendente que Tukey Lambda no se use para el modelado estadístico debido a la falta de un PDF o CDF fácilmente definible. Su uso principal es aproximar otras distribuciones de probabilidad simétricas como:
- Distribución de Cauchy (λ = -1)
- Distribución normal (λ = 0,14)
- Distribución en forma de U (λ = 0,5)
También es una coincidencia exacta para algunas distribuciones, que incluyen:
- Distribución logística (λ = 0)
- Distribución uniforme (λ = -1 a 1)
Orígenes
La distribución lambda de Tukey fue propuesta por primera vez por John Tukey en 1960 (aunque se basó en el trabajo de 1947 de Hastings et. al). A principios de la década de 1970, John Ramberg y Bruce Schmeiser generalizaron la distribución para su uso en simulaciones de Monte Carlo ; Ramberg y sus colegas continuaron desarrollando las propiedades de ajuste de curvas de la distribución a finales de los años 70. Después de ajustar la curva, puede modelar los residuos de esa curva. Los algoritmos de ajuste de curvas incluyen: descenso de gradiente, Gauss-Newton y el algoritmo de Levenberg-Marquardt .
Diagrama de PPCC de Tukey-Lambda
Uno de los usos más comunes de la distribución Tukey-Lambda es en la generación de gráficos PPCC. Un gráfico PPCC de Tukey-Lambda (Gráfico de Coeficiente de Correlación de Gráfico de Probabilidad) es generado por software y se basa en un conjunto de datos ingresados. La gráfica da como resultado un modelo sugerido para los datos.
Referencias :
Tukey, J. (1960). La relación práctica entre las transformaciones comunes de porcentajes de cuentas y cantidades, Informe técnico 36. Grupo de investigación de técnicas estadísticas, Universidad de Princeton.
Hastings, C. et. al (1947). Momentos bajos para muestras pequeñas: un estudio comparativo de estadísticas. Anales de Estadística Matemática, 18, 413-426.
Karian, Z. (2000). Ajuste de distribuciones estadísticas: la distribución Lambda generalizada y los métodos Bootstrap generalizados, 1.ª edición. Chapman y Hall/CRC
Ramberg, J & Schmeiser, B. (1972). Un método aproximado para generar variables aleatorias simétricas. común ACM, 15:987-990.
Ramberg, J. et. Alabama. (1979). Una distribución de probabilidad y sus usos en el ajuste de datos. Technometrics, 21(2):201-214, mayo de 1979.

