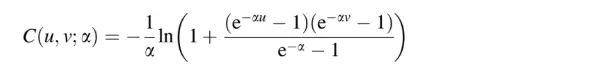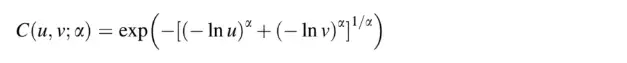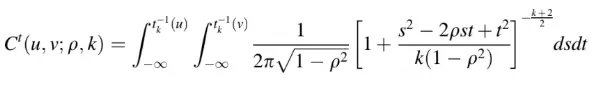Contenido de este artículo
Actualizado el 16 de mayo de 2022, por Luis Benites.
Las distribuciones de cópula contienen cópulas (del latín link ), las distribuciones conjuntas de variables aleatorias . Nos permiten identificar dependencias en distribuciones multivariadas ; Cualquier distribución multivariante se puede modelar con un conjunto especificado por separado de distribuciones marginales y la cópula.
Cada variable aleatoria U 1 , U 2 , …, Up tiene una distribución uniforme marginal U ( 0, 1).
Las cópulas y las distribuciones de cópulas se utilizan en muchas áreas de las estadísticas y las finanzas. Por ejemplo, las cópulas juegan un papel clave en la fijación de precios de valores (Haugh, 2016). En el análisis de riesgos , la selección de modelos para las distribuciones de Copula se puede utilizar para vincular múltiples procesos de riesgo (Cruz et al., 2015).
En lingüística , las cópulas gramaticales unen partes de una oración. Aunque comparten el mismo nombre, matemáticamente no están relacionados.
Tipos de distribuciones de cópula
La familia de distribuciones de cópula incluye una amplia variedad de funciones con diferentes comportamientos de cola. Cuatro de las funciones de Cópula más comunes, junto con sus respectivas Funciones de Densidad de Probabilidad son (Xue et al, 2019):
- Función de distribución binaria de Clayton Copula: esta variante tiene una cola asimétrica con un coeficiente de correlación de cola superior de cero. Es adecuado para encontrar la correlación de cola inferior entre variables:
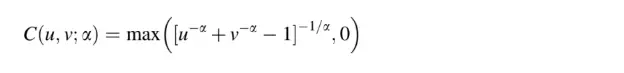
- Función de distribución binaria de Frank Copula : este tipo tiene una cola independiente simétrica con coeficientes de correlación de cero para ambas colas:

- Función de distribución binaria de cópula de Gumbel : este tipo tiene una cola asimétrica con un coeficiente de correlación de cola inferior de cero. Es adecuado para calcular la correlación de cola superior entre variables:

- Función de distribución de cópula binaria t-student : esta variante tiene una cola simétrica gruesa, tan sensible a los cambios en las variables aleatorias que afectan a las colas.

Referencias
Cruz, M. et al. (2015). Aspectos fundamentales del riesgo operativo y análisis de seguros: un manual de riesgo operativo (Manuales de Wiley en ingeniería financiera y econometría) 1.ª edición. Wiley.
Gupta, A. 2013. Gestión de Riesgos y Simulación 1ª Edición . Prensa CRC.
Haugh, M. (2016). Introducción a las cópulas. Recuperado el 13 de abril de 2019 de: An http://www.columbia.edu/~mh2078/QRM/Copulas.pdf
Xue et al. (2019). Actas del FORO PURPLE MOUNTAIN 2019: Foro internacional sobre protección y control de redes inteligentes, Volumen 2. Springer.
¿Te hemos ayudado?
Ayudanos ahora tú, dejanos un comentario de agradecimiento, nos ayuda a motivarnos y si te es viable puedes hacer una donación:La ayuda no cuesta nada
Por otro lado te rogamos que compartas nuestro sitio con tus amigos, compañeros de clase y colegas, la educación de calidad y gratuita debe ser difundida, recuerdalo: